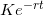
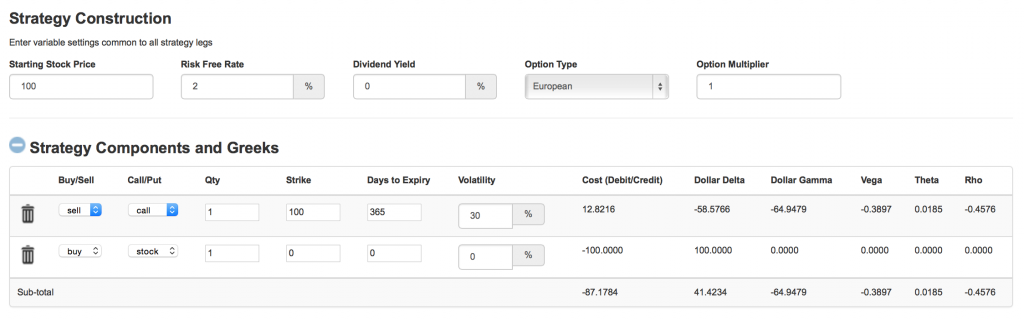
本文节选自权翼《备兑开仓白皮书》。 备兑开仓策略是比较简单且风险较低的期权策略，很多投资者，包括金融机构，经常使用这一策略来增加持仓股票的收益。 什么是备兑开仓策略？ CoveredCall=LongStock+ShortCall 即：备兑开仓由买入标的股票并同时卖出看涨期权组成 当投资者已经拥有标的股票，以卖出看涨期权为开仓方式的操作，称为备兑开仓 当投资者不拥有标[阅读全文]
权翼
金融产品的量化分析
博文
(2016-03-01 09:37:46)
本文节选自权翼《备兑开仓白皮书》。 备兑开仓策略是比较简单且风险较低的期权策略，很多投资者，包括金融机构，经常使用这一策略来增加持仓股票的收益。 什么是备兑开仓策略？ CoveredCall=LongStock+ShortCall 即：备兑开仓由买入标的股票并同时卖出看涨期权组成 当投资者已经拥有标的股票，以卖出看涨期权为开仓方式的操作，称为备兑开仓 当投资者不拥有标[阅读全文]
(2016-02-29 07:52:24)
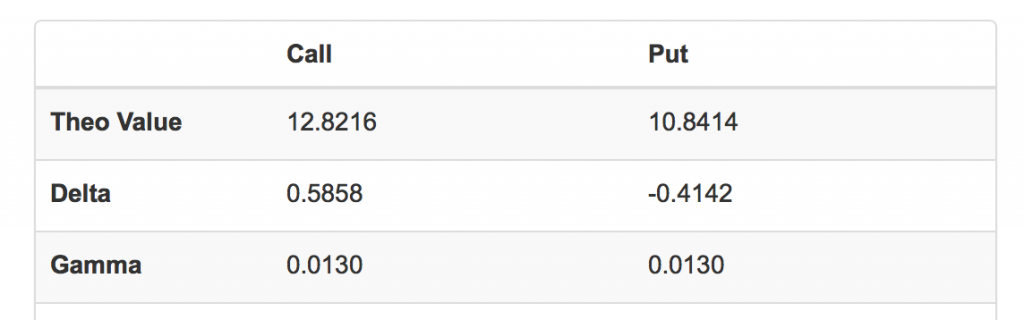
上篇帖子中，我们为读者讲解了作为期权风险系数的希腊字母中的第一个字母Delta。 读者还记得Delta是期权价格相对于标的股票价格变化的敏感度。期权的Delta不是固定不变的，会随标的股票价格、波动率、股息率、和无风险利率等其它变量变化而变化。而在期权风险系数中描述Delta相对于标的股票价格变化的敏感度，就是我们这一节的主题：Gamma。 Gamma的定义 Gamma的理论[阅读全文]
(2016-02-26 07:06:53)
VIX是描述S&P500指数的波动率指标。
对于个股期权交易，我们要随时把握个股期权序列的整体波动率水平。
近似于VIX，个股短期波动率指数，以单一的指数形式，为期权投资者分析波动率、构建交易组合，提供了重要的决策依据。
下面是短期个股波动率指数的样本数据。
短期个股波动率指数
股票代码
交易日
IVShortTermIndex
[阅读全文]
(2016-02-25 09:12:48)
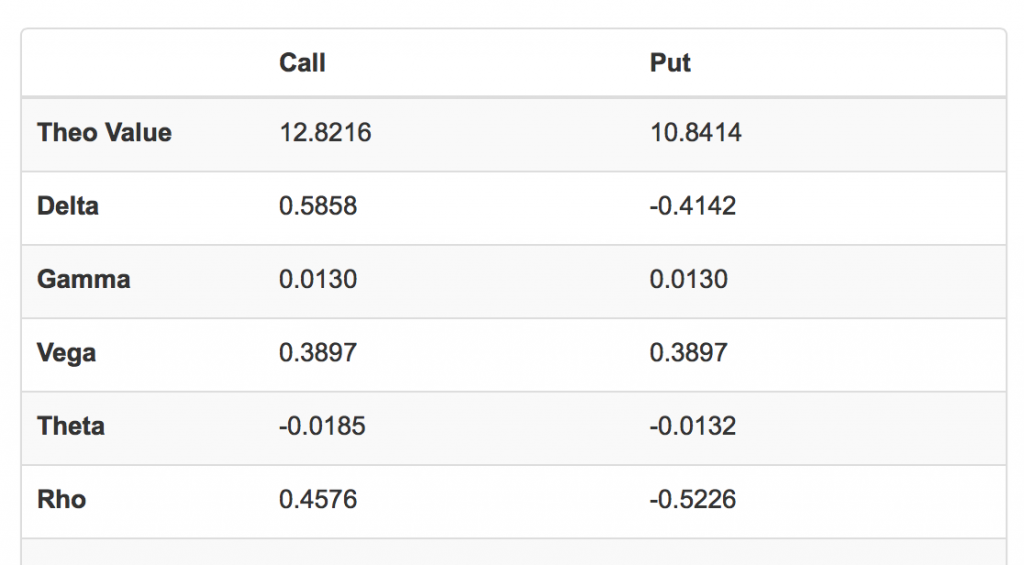
前两篇文章中，我们讲解了如何利用期权计算器来计算期权价格，如何由期权的市场价格反向计算隐含波动率。读者在学习的过程中，可能已经逐渐意识到期权的交易机会就在计量分析的能力当中。 在期权计算器中，我们还有一个重要的功能没有涉及，这就是代表期权不同风险系数的希腊字母。下图就是权翼的期权计算器在默认页面显示的希腊字母输出内容： 还不太[阅读全文]
(2016-02-24 06:15:52)
上一贴我们讲解如何用期权计算器验证期权的平价关系，并如何利用平价关系获取市场套利的交易机会。虽然实践中作为普通投资者，几乎没有可能有效地实施这一交易进行套利，但正是因为这些特性的存在，使得资本市场成为高效市场；具有交易优势的机构或个人，利用高级的算法和计算能力，可以迅速捕捉交易信号，研发出真正的交易策略。 其实学习期权的过程就是寻[阅读全文]
(2016-02-23 07:08:13)
期权计算器是学习期权理论跨向实践的第一步。看似简单的运算功能，其实包含了期权的众多特性，勤学苦练一定能悟出很多交易技巧。 从期权基础知识中，我们知道期权的价格相对于标的股票价格的变动是非线性的。多种因素会影响期权价格，比如：标的股票价格，还受制于无风险利率、期权有效期、行权价、股息、和波动率等。因此投资者很难从标的股票价格的变动[阅读全文]
(2016-02-22 13:36:40)
依赖Black-Sholes-Merton估值模型，如果将期权的市场价格作为已知参数，我们可以反向推算出波动率。不同于靠股票历史价格计算出的历史波动率，我们将由市场价格推算出的波动率称为隐含波动率，既由期权价格所隐含的波动率。
波动率曲面
对于同一标的股票，用不同的到期日以及不同的行权价的多个期权的市场价格反向推算出的隐含波动率数值通常是不同的；以到期日[阅读全文]
(2016-02-22 13:35:54)
期权价格取决于下列参数：
无风险利率(Risk-FreeRate)
标的资产价格(StockPrice)
距到期日时间(Maturity)
标的股息年化率(DividendYield)
标的价格波动率(Volatility)
期权行权价格(StrikePrice)
针对于每项参数变化而引起的期权价格变化的敏感度，我们定义为一个希腊字母，用于量化描述期权包含的风险系数。希腊字母有多个，下面介绍常用的几个。
Delta为期权价格相[阅读全文]
(2016-02-22 13:33:51)
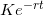
在期权的研究理论体系里，关于看涨期权与看跌期权，有一个重要的平价关系。 假设两个投资组合： 一个欧式看涨期权，和等值于的现金 一个欧式看跌期权，和一份（等数量）股票 (K代表行权价，r代表无风险利率) 我们可以看出，两个投资组合在期权到期日的价值相同，均为： max(ST,K) (ST代表到期日标的价格) 因此两个组合当前的价值也应当相同；也就是[阅读全文]
(2016-02-22 13:32:46)
通常我们谈论期权价格时会涉及到两个数值：期权的市场价格，和期权的理论估值。
期权是市场交易产品，因此从市场上直接观测到的成交价格，就是期权的市场价格。
而期权的理论价值却是用数学模型计算出的结果。前文介绍了影响期权价值的六个因子。基于数学模型，在输入期权的六个定价因子后得出的期权价格，我们称为期权的理论估值。使问题变得更为复杂[阅读全文]
