权翼

金融产品的量化分析

首页文章列表博文目录

个人资料

权翼

给我悄悄话

博客访问：

VIX指数衍生品交易技术分析篇 VXX/XIV的量化分析演示

(2017-03-01 14:30:07) 下一个

VXX／XIV量化分析演示

(因为黏贴关系，格式有所变化，原文可以参照optionwings.com网站策略研发->VXX/XIV量化分析演示)

本节讲解并通过Python代码逐步验证Tony Cooper关于VIX衍生品VXX及XIV的量化分析方法和实践策略

原论文请参考：

Easy Volatility Investing： Tony Cooper, Feb 2013

简介

该论文尝试以波动率指数(VIX Index)衍生的ETP产品建立波动率投资策略。

论文结构大致如下：

波动率收益从何而来？
5种交易策略
波动率资产类别作为投资组合中分散投资的优势

1. 引言

论文总结了以下几点VIX波动率指数的既有规律(典型化事实)：

VIX不同于普通股票，一定程度上是可以预测的
VIX日变化率与股指日收益率具有负相关性
投资者以付保费的方式规避波动率风险

论文目录

波动率风险风险溢价(Volatility Risk Premium - VRP)，而不是滚动收益(roll yield)，提供了波动率投资收益
波动率指数ETPs: VXX/XIV
交易策略
交易风险:
- 波动率拖拉风险(Volatility Drag)
- 时间同步风险(Timing Synchronization)
- 波动率风险溢价与滚动收益的聚合风险(VRP-Roll Yield Convergence)
- VIX体制变化风险(Regime Change Risk)
- 压路机风险(Steamrollr Risk)
利用波动率ETP分散投资风险
- 与S&P500的低相关性
- 提高收益
- 降低波动率
- 减少回撤
- 改善Sharpe

2. 波动率的诱惑

关于CBOE VIX指数，我们在VIX衍生品系列讲座中已经涉及( http://bit.ly/2lcQIEb)，这里不再重复,着重陈述一下论文中的观点。

论文认为：VIX是可以预测的，这是基于VIX具有均值回归特性这一假设作出的推断。

简单的基于11日均值回归的策略可以获得215%的年化收益(当VIX低于11日均线时做多，当VIX高于11日均线时做空)

论文指出：VIX的变化与S&P500的变化为负相关

这意为着：如果通过VIX交易可以获得正收益，就可以为投资组合进行分散投资

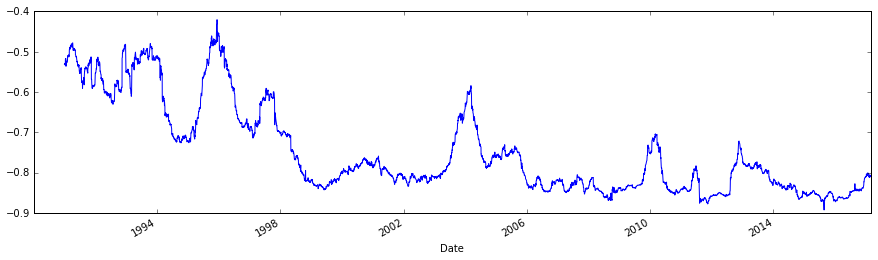
下图是我们用Python代码进行的验证，图形显示VIX与S&P指数SPX日收益的移动一年相关系数。注意二者负相关性逐渐趋强。

In [2]:

import pandas as pd

import pandas_datareader as web

import numpy as np

import matplotlib.pyplot as plt

% matplotlib inline

vix = web . DataReader( '^vix' , 'yahoo' , '1990-01-01' )

spx = web . DataReader( '^GSPC' , 'yahoo' , '1990-01-01' )

xiv = web . DataReader( 'xiv' , 'yahoo' , '2010-10-30' )

data = pd . DataFrame()

data[ 'VIX' ] = vix[ 'Adj Close' ]

data[ 'SPX' ] = spx[ 'Adj Close' ]

data[ 'XIV' ] = xiv[ 'Adj Close' ]

data[ 'VIX_Ret' ] = data[ 'VIX' ] . pct_change()

data[ 'SPX_Ret' ] = data[ 'SPX' ] . pct_change()

data[ 'VIX_Ret' ] . rolling( 252 ) . corr(data[ 'SPX_Ret' ]) . plot(figsize = ( 15 , 4 ))

Out[2]:

论文中展示VIX和XIV在2012-04-03至2012-10-01间的走势图，我们用以下代码实现。

In [3]:

data_scaled = pd . DataFrame()

data_scaled[ 'VIX' ] = data[ 'VIX' ] / data . ix[ '2012-04-03' ][ 'VIX' ]

data_scaled[ 'XIV' ] = data[ 'XIV' ] / data . ix[ '2012-04-03' ][ 'XIV' ]

data_scaled . ix[ '2012-04-01' : '2012-10-01' ][[ 'VIX' , 'XIV' ]] . plot(figsize = ( 15 , 8 ))

Out[3]:

如上图所示，期间VIX基本回到初始值，但XIV升幅近40%。

3. 波动率风险溢价(The Volatility Risk Premium)

论文在这一章节主要解释及论证VRP的存在。

论文认为：在波动率交易双方，对冲套保交易员情愿付钱给投机交易员，用于减少自身的波动率风险。

VRP代表VIX指数对S&P500波动率的预测的超额部分(关于VIX指数，请参考http://bit.ly/2mL94IQ )
下图是我们用Python代码展示的VIX即期与30天后实现的SPX历史波动率(我们用21个交易日代替30个自然日)
从图中可以明显看出，VIX在多数时间里高于30天后的历史波动率
论文认为，这意味着VRP在多数时间里为正

In [4]:

data[ 'SPX_HV21' ] = data[ 'SPX_Ret' ] . rolling( 21 ) . std() * np . sqrt( 252 ) * 100

data[ 'SPX_HV21_Shift' ] = data[ 'SPX_HV21' ] . shift( -21 )

data[[ 'VIX' , 'SPX_HV21_Shift' ]] . plot(figsize = ( 15 , 8 ))

Out[4]:

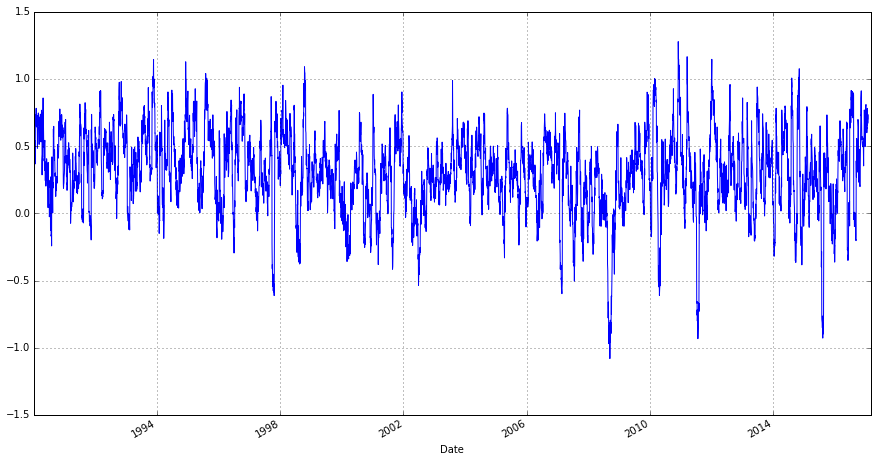
我们进一步用下图显示二者之间的差异。按论文陈述，我们取二者对数差，使显示更加清晰。

In [5]:

(np . log(data[ 'VIX' ]) - np . log(data[ 'SPX_HV21_Shift' ])) . plot(figsize = ( 15 , 8 ),grid =1 )

Out[5]:

4. VIX期货

关于VIX期货，读者可以参考我们的专题( http://bit.ly/2lX0iIF)。

VIX衍生品ETP是建立在VIX期货基础上的。因为VIX指数没有现货产品，不能直接交易，因此VIX期货价格代表市场对未来VIX水平的共同期待值。

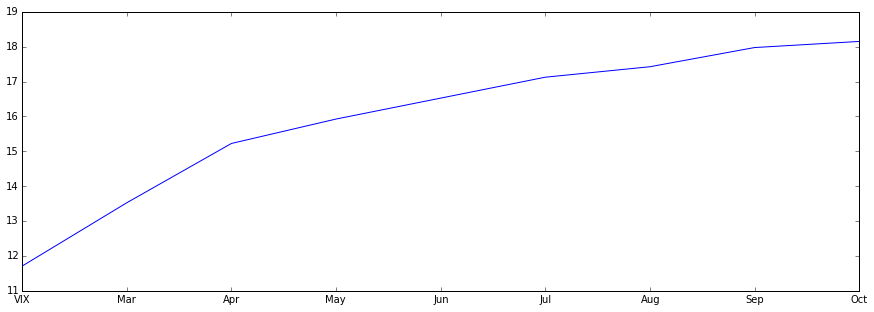
下图显示的是2017年2月23日VIX期货的展期结构曲线，这一天呈明显的溢价形态(Contango)。

In [6]:

import sys

sys . path . append( "/Users/valley11/Google Drive/Projects/Python/Samples" )

import cboe_vx as cboe

VXF = pd . DataFrame()

VXF[ 'VIX' ] = data[ 'VIX' ]

f = cboe . getCboeData( 2017 , 3 )

VXF[ 'Mar' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2017 , 4 )

VXF[ 'Apr' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2017 , 5 )

VXF[ 'May' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2017 , 6 )

VXF[ 'Jun' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2017 , 7 )

VXF[ 'Jul' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2017 , 8 )

VXF[ 'Aug' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2017 , 9 )

VXF[ 'Sep' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2017 , 10 )

VXF[ 'Oct' ] = f[ 'Settle' ]

VXF . ix[ '2017-02-23' ] . plot(figsize = ( 15 , 5 ))

Out[6]:

下图我们再展示历史上展期结构呈逆向形态的曲线，这是发生在金融危机中的2008年10月3日。

In [7]:

VXF = pd . DataFrame()

VXF[ 'VIX' ] = data[ 'VIX' ]

f = cboe . getCboeData( 2008 , 10 )

VXF[ 'Oct' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2008 , 11 )

VXF[ 'Nov' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2008 , 12 )

VXF[ 'Dec' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2009 , 1 )

VXF[ 'Jan' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2009 , 2 )

VXF[ 'Feb' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2009 , 3 )

VXF[ 'Mar' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2009 , 4 )

VXF[ 'Apr' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2009 , 5 )

VXF[ 'May' ] = f[ 'Settle' ]

f = cboe . getCboeData( 2009 , 6 )

VXF[ 'Jun' ] = f[ 'Settle' ]

VXF . ix[ '2008-10-03' ] . plot(figsize = ( 15 , 5 ))

Out[7]:

前文通过VIX与SPX历史波动率的比对，论证了VRP的存在；但因为VIX不可直接交易，无法获取这一交易优势。

在介绍VIX期货后，论文提出问题：VRP在VIX期货市场中存在么？

这个验证有点难度，因为VIX期货产品距到期日时间是逐渐减少的，无法用VIX即期价格(30日估值)和没有准确时间的期货直接比较。

论文借鉴了S&P500 VIX短期期货指数的一个方法，即建立一个假设的恒定一个月到期的VIX期货产品，该期货30天后会以当时VIX即期作为结算价格。因此恒定一个月到期的期货与30天后的VIX之间具有了可比性。

下面的代码及图形尝试描述两者间的关系：

恒定一个月到期期货有实际交易的首月(F1)及第二月(F2)期货按时间加权平均获得
VIX前移30天(21个交易日)

In [8]:

import Quandl

VXF30 = pd . DataFrame()

x = Quandl . get( "CHRIS/CBOE_VX1" ) # continuous F1

VXF30[ 'F1' ] = x[ 'Settle' ]

x = Quandl . get( "CHRIS/CBOE_VX2" ) # continuous F2

VXF30[ 'F2' ] = x[ 'Settle' ]

calendar = pd . read_csv( 'f1_f2_ttm.csv' ) # read in expiry dates and days till maturity

calendar = calendar . set_index( 'Date' )

VXF30 = pd . merge(VXF30, calendar, how = 'left' , left_index = True , right_index = True )

VXF30[ 'X1' ] = 30 - VXF30[ 'TTM1' ]

VXF30[ 'X2' ] = VXF30[ 'TTM2' ] - 30

VXF30[ 'W1' ] = VXF30[ 'X2' ] / (VXF30[ 'X1' ] + VXF30[ 'X2' ])

VXF30[ 'W2' ] = VXF30[ 'X1' ] / (VXF30[ 'X1' ] + VXF30[ 'X2' ])

VXF30[ 'VXF30' ] = VXF30[ 'F1' ] * VXF30[ 'W1' ] + VXF30[ 'F2' ] * VXF30[ 'W2' ]

VXF30[ 'VIX' ] = data[ 'VIX' ]

VXF30[ 'VIX_ShiftF21' ] = data[ 'VIX' ] . shift( -21 )

#VXF30['VIX'] = data['VIX'].shift(-21)

VXF30[[ 'VXF30' , 'VIX_ShiftF21' ]] . ix[ '2007-10-01' :] . plot(figsize = ( 15 , 8 ))

Out[8]:

可以看出，多数时间里，假设的恒定30天期货价格高于30天后VIX的即期价格。

论文认为这意味着VRP在VIX期货市场中同样存在。

下图进一步显示二者间的对数差。

In [9]:

(np . log(VXF30[ 'VXF30' ] . ix[ '2007-10-01' :]) - np . log(VXF30[ 'VIX_ShiftF21' ] . ix[ '2007-10-01' :])) . plot(figsize = ( 15 , 8 ),grid = True )

(np . log(VXF30[ 'VXF30' ] . ix[ '2007-10-01' :]) - np . log(VXF30[ 'VIX_ShiftF21' ] . ix[ '2007-10-01' :])) . mean()

Out[9]:

0.07111734832772859

5. 滚动收益(Roll Yield)

在明确了VIX与VIX期货间的关系后，论文提出以下问题：

在VIX即期与期货二者动态关系中，是即期价格向期货价格聚合靠拢，还是期货价格向即期价格聚合靠拢？

这个问题实际就是即期与期货，哪个对预测未来波动率更有效。

论文继续陈述以下观点：

－滚动收益描述的是VIX即期与期货价格之间的差值

－滚动收益可以精确测量，但VRP不能

－当期货展期呈溢价形态(Contango)时，滚动收益为正；反之为负

我们用下图显示滚动收益的表现。

In [11]:

VXF[ 'F1_VIX_Yield' ] = (VXF30[ 'F1' ] - VXF30[ 'VIX' ]) / VXF30[ 'VIX' ] / VXF30[ 'TTM1' ]

VXF[ 'F1_VIX_Yield' ] . ix[ '2007-10-01' :] . plot(figsize = ( 15 , 8 ),grid = True )

Out[11]:

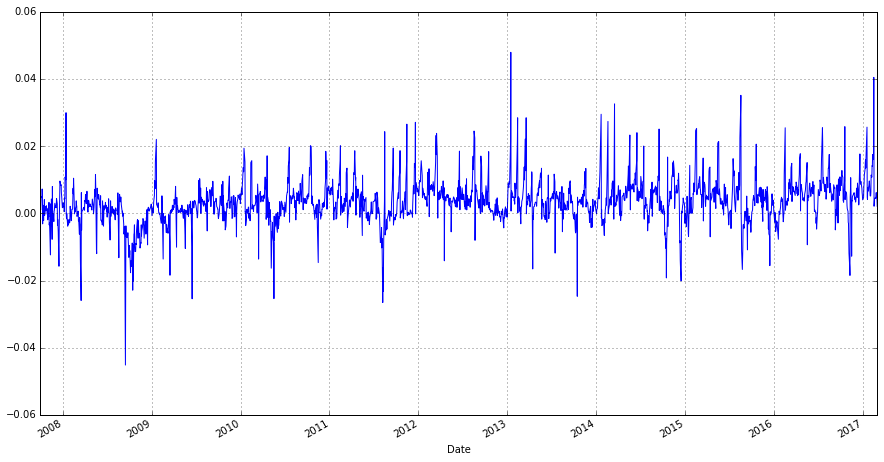
从2007年10月1日至今，首月期货与即期价格间的滚动收益率日均大约为0.34%，相当于每月7%。

In [12]:

VXF[ 'F1_VIX_Yield' ] . ix[ '2007-10-01' :] . mean()

Out[12]:

0.0033657100890936895

6. 基于VIX期货的ETP产品

关于基于VIX期货的ETP产品，我们有专题讲解，这里不做过多陈述。简单列举论文中涉及的几个产品。

基于S&P 500 VIX短期期货指数的ETP：正向VXX，反向XIV

基于S&P 500 VIX中期期货指数的ETP：正向VXZ，反向ZIV

除此以外，还有很多正向、反向、单倍、与多倍的ETP产品，但基本遵从非常近似的产品结构。

7. XIV 动态特性

XIV的产品设计为跟踪S&P500 VIX短期期货指数，希望通过持有VIX前两个月期货的空仓，实现每日反向的指数收益率：

即当期货下跌时，XIV上涨；反之亦然
因为VIX期货与VIX即期具有正相关性，通常VIX即期下跌时，XIV上涨(并非所有时候)

XIV每日在第一与第二月期货产品间调仓，维持恒定的一个月到期的期货。

下面我们用Python代码展示XIV相对于VIX的回归分析。

In [14]:

import OLS_Regression as ols

data[ 'XIV_Ret' ] = data[ 'XIV' ] . pct_change()

ols . linreg(data[ 'VIX_Ret' ] . ix[ '2010-12-01' :] . values, data[ 'XIV_Ret' ] . ix[ '2010-12-01' :] . values)

Out[14]:

OLS Regression Results

Dep. Variable:	y	R-squared:	0.777
Model:	OLS	Adj. R-squared:	0.777
Method:	Least Squares	F-statistic:	5466.
Date:	Wed, 01 Mar 2017	Prob (F-statistic):	0.00
Time:	13:02:31	Log-Likelihood:	3990.8
No. Observations:	1571	AIC:	-7978.
Df Residuals:	1569	BIC:	-7967.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[95.0% Conf. Int.]
const	0.0032	0.000	6.584	0.000	0.002 0.004
x1	-0.4613	0.006	-73.930	0.000	-0.474 -0.449

Omnibus:	325.865	Durbin-Watson:	2.115
Prob(Omnibus):	0.000	Jarque-Bera (JB):	2968.399
Skew:	-0.697	Prob(JB):	0.00
Kurtosis:	9.588	Cond. No.	13.0

论文进一步定义：

XIV日滚动收益期待值＝ (F2 - F1)/F1/30

下图我们尝试绘制该期待值自XIV发布以来的时间序列以及累计效果。

In [15]:

VXF30[ 'F2_F1_Yield' ] = (VXF30[ 'F2' ] - VXF30[ 'F1' ]) / (VXF30[ 'F1' ]) /30

(VXF30[ 'F2_F1_Yield' ] . ix[ '2010-10-30' :] *100 ) . plot(figsize = ( 15 , 8 ), grid = True )

Out[15]:

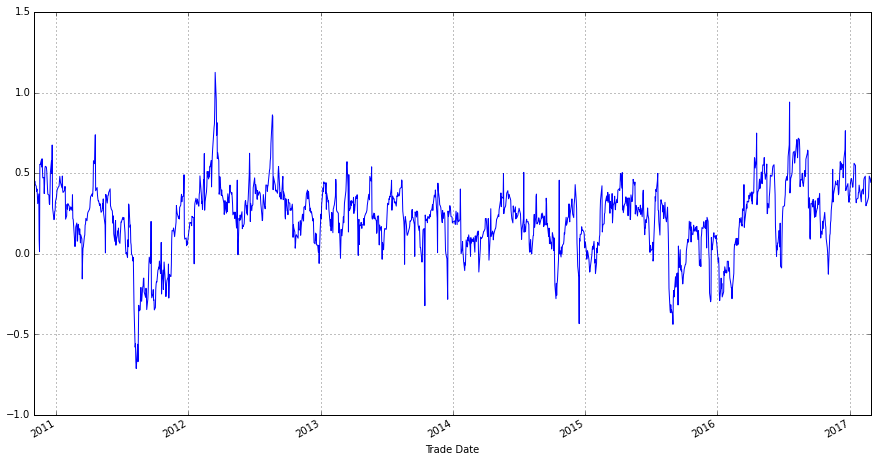
上图同时清晰的显示了首月与次月呈溢价与逆向结构的阶段：

曲线位于0以上的日期，首月与次月为溢价结构(Contango)
曲线位于0以下的日期，首月与次月为逆向结构(Backwardation)

In [240]:

VXF30[ 'F2_F1_Yield' ] . ix[ '2010-10-30' :] . add( 1 ) . cumprod() . plot(figsize = ( 15 , 8 ),grid = True )

Out[240]:

上图为日滚动收益期待值的累积效果。如图所示，如果滚动收益的期待值可以实现，XIV会在短短几年获得巨大收益。显然，事实并非如此。

8. 更多的XIV动态特性

我们先展示VXX与XIV自发布之日起至今的2009-01-29与2010-11-30间的走势图。

In [16]:

data[ 'VXX' ] = web . DataReader( 'vxx' , 'yahoo' , '2009-01-29' )[ 'Adj Close' ]

data[[ 'VXX' ]] . ix[ '2009-01-29' :] . plot(figsize = ( 15 , 4 ))

Out[16]:

In [17]:

data[[ 'XIV' ]] . ix[ '2010-11-30' :] . plot(figsize = ( 15 , 4 ))

Out[17]:

从上面两个图，我们看出：

XIV与VXX为反向发展，但XIV上升幅度远远不如VXX下降幅度
这是由于反向收益的复利累计所致
同时波动率拖拉也造成对多倍与反向ETF有很大阻碍作用
XIV最大的单日损失为-26.8%，发生在2016年6月24日
XIV最大回撤为-74%，发生于2011年7月7日与2011年11月25日期间
按论文所述，如果用VIX期货价格反向倒推XIV价格至2004年，则XIV最大回撤在金融危机期间，回撤值为-93%

下面我们用代码演示回撤计算。

In [22]:

ret = data[ 'XIV_Ret' ] . add( 1 ) . cumprod()

dd = ret . div(ret . cummax()) . sub( 1 )

mdd = dd . min()

end = dd . argmin()

start = ret . loc[:end] . argmax()

print "Maximum Drawdown:" , mdd

print "Peak Date:" , start

print "Trough Date:" , end

Maximum Drawdown: -0.743870631195

Peak Date: 2011-07-07 00:00:00

Trough Date: 2011-11-25 00:00:00

9. 交易策略

论文阐述了5种交易策略，每种策略包含多种交易信号。

策略一：买入持有

这与上面绘制的XIV走势曲线基本一致
自发布日至今，年化收益在30+%
该策略回撤风险很大

策略二：动量策略

(i) 计算并比较过去k日中收益最高的ETN，买入并持有

(ii) 当所有k日收益为零，保持空仓

论文建议使用83天作为参数。

策略三：溢价／逆向滚动收益策略(Contango-Backwardation Roll Yield)

策略寻求获取最大的滚动收益：在展期为溢价(Contango)时，买入XIV，当展期为逆向(Backwardation)时，买入VXX

该策略信号清晰，比较容易把握(VXV为90日波动率指数):

VXV > VIX：买入XIV，卖出VXX
VXV < VIX：买入VXX，卖出XIV

论文同时给出多个信号变种：

Vratio - VXV/VIX：使用中，用10日均线做平滑处理
ERY：期待滚动市盈率
T1ratio - VIX1/VIX：恒定一个月期货相对于VIX即期
T2ratio - VIX2/VIX：恒定两个月期货相对于VIX即期
T5ratio - VIX5/VIX
T51ratio - VIX5/VIX1
T52ratio - VIX5/VIX2
T21ratio - VIX2/VIX1

论文建议使用Vratio或10日均值的Vratio10

策略四：波动率风险溢价(Volatility Risk Premium)

信号组合：

HVOL21: spot VIX - HV21 (VIX即期－ SPX21日历史波动率)
HVOL10: spot VIX - HV10 (VIX即期－ SPX10日历史波动率)
HVOL10S: spot VIX - HV10(10日历史波动率附加5日移动平均做光滑处理)
EGARCH: spot VIX - EGARCH(1,1) (VIX即期－ EGARCH估值)
EGARCH1: VIX1 - EGARCH(1,1)
EGARCH2: VIX2 - EGARCH(1,1)
EGARCH5: VIX5 - EGARCH(1,1)
VRPO21: SPX期权市场在21个交易日前实现的VRP
VRPF21: VIX期货市场在21个交易日前实现的VRP

论文推荐使用HVOL10S，即10日历史波动率附加5日移动平均值

策略五：对冲

该策略对于ETN的发行者有利，因为涉及持续的对冲与调仓，我们不做过多解释。

其它策略

既然波动率拖拉对XIV投资有阻碍作用，论文建议可以讲VIX本事波动率引入策略开发之中，用来提高收益。例如：

stdlVIX 定义为VIX对数的标准差，对上述策略的一个改进就是：

当Vratio > 1，并且在stdlVIX < 0.14，买入XIV。

10. 交易风险

论文提到上述策略在截止至2013年2月的历史回测中都获得了很好的收益。我们需要指出，2013年以前和以后的波动率市场不尽相同，如果回测自VXX/XIV发布之日至今，结论并不一致。我们本节的讲解主要针对熟悉分析方法，所以并不做过多评论。

在探讨交易风险时，论文主要谈及以下两个方面：

1) 未来难以获得同样收益的风险(类似于统计中的过度适应问题Overfitting)

2) 将这些策略引入已有投资组合中的带来的裨益

VRP会持续么？论文认为：

投资者会继续愿意付出溢价(相对于保费)来让交易对手承担自己的波动率风险
VRP的规模可能会减少，因为更多的人意识到这个交易优势，从而减少收益
监管部门可能对VIX ETP产品进行约束与限制，因为这些ETP产品通过反馈机制影响VIX水平及SPX期权波动率，引起更加频繁的高波动率事件

论文列举以下几点实证分析中的风险因素：

波动率拖拉
时间同步
VRP滚动收益风险
VIX体制变化风险
回撤风险(压路机风险)

波动率拖拉

波动率指的是日收益率的年化波动率。

论文指出，当日收益率的波动率增加时，复利累计的收益会减少，也就是收益率波动率越高，累计收益越低。

我们参考下图。

In [23]:

data . ix[ '2012-03-25' : '2012-08-15' ][[ 'VIX' , 'XIV' ]] . plot(figsize = ( 15 , 8 ))

Out[23]:

上图显示的是VIX指数与XIV在2012年3月25日至2012年8月15日间的走势图。论文指出：

VIX指数在结束时基本收平，这意味着VIX对XIV的收益没有影响
同时这也意味着XIV的收益应当来源于滚动收益

下面我们分析期间的滚动收益。

In [24]:

VXF30 . ix[ '2012-03-25' : '2012-08-15' ][ 'F2_F1_Yield' ] . plot(figsize = ( 15 , 4 ))

VXF30 . ix[ '2012-03-25' : '2012-08-15' ][ 'F2_F1_Yield' ] . mean()

Out[24]:

0.0032925691048866844

如上图所示，日滚动收益的期待值非常显着：

期待值从未低于零
因此我们应该期待XIV获得很大的收益

我们再用下图展示VIX，首月F1，次月F2期货在此期间的走势。

In [25]:

data = pd . merge(data, VXF30[[ 'F1' , 'F2' , 'F2_F1_Yield' ]], how = 'left' ,left_index = True ,right_index = True )

data . ix[ '2012-03-25' : '2012-08-15' ][[ 'F1' , 'F2' , 'VIX' ]] . plot(figsize = ( 15 , 8 ))

Out[25]:

联系上面三张图，我们很难解释为什么XIV在此期间收益几乎为零。

论文指出，其中的原因是因为波动率拖拉抵消了滚动收益。

关于波动率拖拉的计量方法，我们这里暂不做详细讨论。

时间同步风险

论文指出：

当展期结构在溢价与逆向间频繁变化时，每次依照信号执行的投资很有可能连续踏空。例如展期每天调转方向，依照信号会造成每日投资损失。

同步风险是周期性风险，只发生在溢价与逆向结构调换的时候。

在操作中，可以用10日均线来避免频繁波动。

VRP／滚动收益风险(VRP-RYR)

论文指出，当我们追求滚动收益，而不是VRP时，我们会面临该风险。虽然两者相关，但这种相关性会弱化或消失－特别是在VIX指数频繁做均值回归运动时(即拒绝滚动收益时)。我们可以尝试这样理解：当展期为溢价时，VIX有上升趋势，但此时我们持仓XIV(做空VIX)；当展期为逆向时，VIX有下降趋势，但此时我们持仓VXX(做多VIX) 。

VIX体制变化

VIX体制是通过观察VIX长期走势图，根据VIX水平及发展方向，大致按时间段区分的具有不同特性的阶段。例如2008年金融危机前后，VIX处于20以上的高位；而2012年后至今，VIX呈下降趋势，并逐渐降至12以下水平。

不同的VIX特性阶段，适用于不同的交易策略。因此判断VIX体制的变化，也是ETP交易的重要一环。论文特此将体制变化最为交易风险之一。

回撤风险

前面论述关于XIV高达－74%的回撤值，充分说明VIX ETP交易属于高风险品种。

11. 分散投资

论文认为VIX衍生品交易可以作为独立投资资产类别，依靠其与股指的负相关性，可以为已有投资组合带来分散投资的优势。论文论证通过上升策略，可以帮助投资组合减少收益波动率，增加收益，减小回撤，提升Sharpe。

12. 未来研究课题

论文探讨通过矢量回归算法预测VRP作为将来的研究课题，希望避免过度适应，提高Sharpe至2～3之间。

13. 总结

总结上述五种策略：

1 - 买入持有

2 - 动量方法

3 - 基于溢价／逆向结构的滚动收益：优势是交易频率非常低，通常一年几次交易

交易信号：当10日移动平均VXV/VIX > 1, 买入XIV; 其它时间：买入VXX

4 - VRP基于波动率风险溢价：交易比较频繁

交易信号：当5日移动平均(VIX - HV10) > 0, 买入XIV; 其它时间：买入VXX

5 - 对冲: 需要频繁调仓，以及特殊软件，适用于ETP发行机构

下面我们举例如何生成交易信号

在交易信号产生后，可以在回测平台(例如Quantopian)进行回测。

In [26]:

# show Vratio10 smoothed by 10 day moving average

# If the 10 day moving average of VXV/VIX > 1, long XIV; otherwise, long VXX

Vratio = pd . DataFrame()

Vratio[ 'VIX' ] = web . DataReader( '^vix' , 'yahoo' , '2000-01-01' )[ 'Adj Close' ]

Vratio[ 'VXV' ] = web . DataReader( '^vxv' , 'yahoo' , '2000-01-01' )[ 'Adj Close' ]

Vratio[ 'VXV/VIX' ] = Vratio[ 'VXV' ] / Vratio[ 'VIX' ]

Vratio[ 'VXV/VIX MA10' ] = Vratio[ 'VXV/VIX' ] . rolling( 10 ) . mean()

Vratio . ix[ '2011-08-01' :][ 'VXV/VIX MA10' ] . plot(figsize = ( 15 , 8 ))

Vratio[ 'VXV/VIX MA10' ] . to_csv( 'vratio_ma10.csv' )

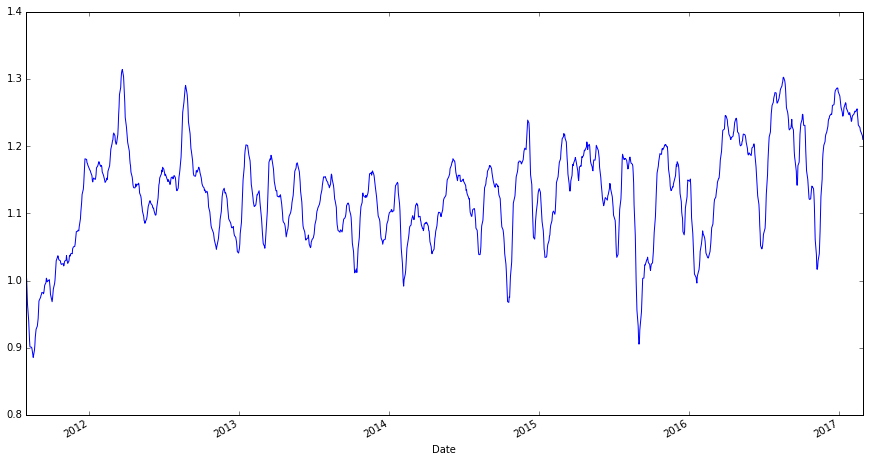
In [27]:

# show VRP

# If the 5 day moving average of (VIX - HV10) > 0, long XIV; otherwise, long VXX

VRP = pd . DataFrame()

VRP[ 'VIX' ] = web . DataReader( '^vix' , 'yahoo' , '2000-01-01' )[ 'Adj Close' ]

VRP[ 'SPX' ] = web . DataReader( '^gspc' , 'yahoo' , '2000-01-01' )[ 'Adj Close' ]

VRP[ 'SPX_Ret' ] = VRP[ 'SPX' ] . pct_change()

VRP[ 'HV10' ] = VRP[ 'SPX_Ret' ] . rolling( 10 ) . std() * np . sqrt( 252 )

VRP[ 'HV10 MA5' ] = VRP[ 'HV10' ] . rolling( 5 ) . mean()

(VRP[ 'VIX' ] - VRP[ 'HV10 MA5' ] *100 ) . plot(figsize = ( 15 , 8 ),grid = True )

(VRP[ 'VIX' ] - VRP[ 'HV10 MA5' ] *100 ) . to_csv( 'vrp_hv10_ma5.csv' )

[ 打印 ]

[ 加入书签 ]

阅读 () ┆ 评论 (0)

目前还没有任何评论

登录后才可评论.

权翼

VIX指数衍生品交易 技术分析篇 VXX/XIV的量化分析演示

VIX指数衍生品交易技术分析篇 VXX/XIV的量化分析演示