权翼
金融产品的量化分析这一节的内容是关于波动率的风险系数:Vega。这也是我们利用期权计算器,来熟悉了解基本希腊字母特性的最后一节。
Rho作为无风险利率变化敏感系数,对期权价格影响较小,我们就不再作单独介绍。
当然,除了Delta, Gamma, Theta, Vega,和Rho之外,还有很多更为复杂的希腊字母,我们保留在将来的高级期权知识中陆续讲解。
对于一直跟随我们的讲解,对期权知识有了一些初步理解的读者,请先思考下面一个简单问题:
看涨期权,在标的股票价格下跌时,期权价格有可能上涨么?
经过前一段的学习,读者应该逐渐学会从风险系数角度思考期权价格了,那么期权价格的涨跌也就不完全归因于标的股票价格了。
如果我们按风险因子逐一分解,就可以得到期权的损益公式:
期权损益=Delta损益+Gamma损益+Vega损益+Theta损益+其它小系数损益
可以想象,对于买入看涨期权,当股票价格下降:我们会做如下判断:
Delta损益:亏损,因为股票下跌
Gamma损益:盈利,因为股票波动
Vega损益:未知,取决于波动率变化
Theta损益:亏损,因为时间损耗
其它小系数损益:暂时忽略不计
由此可见,如果Vega出现盈利,和Gamma盈利累计,可以弥补Delta与Theta亏损的话,期权整体是有可能盈利的。
下面我们通过一个实例来验证。
请读者打开期权计算器,并输入以下定价参数:
股票价格(Stock):100
行权价(Strike):100
波动率(Volatility):20%
距到期日时间(Time to Maturity):30 天
其它参数保存默认
计算后,我们得到看涨期权价格为2.37。
假设第二天开盘时,受负面消息影响,股票跳空下跌5%开盘,同时市场恐慌情绪加剧,促使隐含波动率迅速飙升至45%。请读者在期权计算器中输入更新后的参数:
股票价格(Stock):95
波动率(Volatility):45%
距到期日时间(Time to Maturity):29 天
重新计算后,我们得到新的看涨期权价格为2.88,高于前一天股票下跌前的价格2.37。
可见,波动率对期权价格的影响不可小觑。事实上,历史上多次恐慌性抛售中,就出现过看涨期权逆势上涨的情况。因此,掌握好Vega和波动率,对期权交易至关重要。
Vega的理论定义
Vega在理论上定义为期权价格相对于标的波动率的变化率。通常我们可以理解为当标的波动率变化一个百分点时,期权价格的变化量。
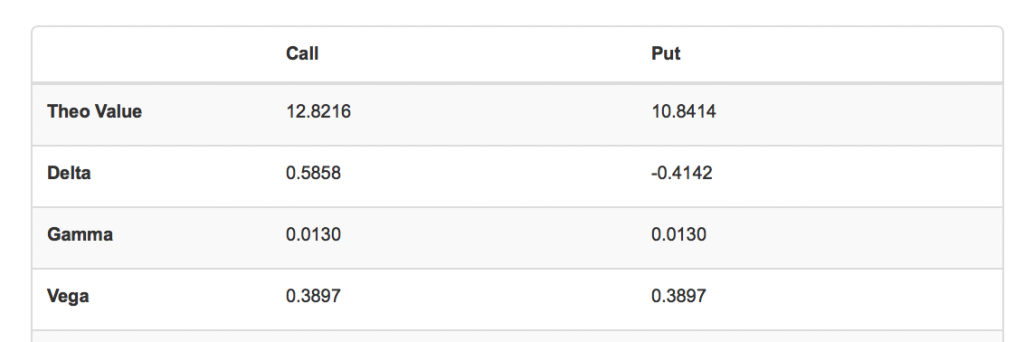
例如,我们使用期权计算器页面的默认数值,可以观察到在波动率为30%时的平值期权波动率为0.3897。
这意味着如果其它变量保持恒定,标的波动率上升或下降一个百分点,即变为31%或29%,期权价格应当相应上升或下降0.3897。我们分别在计算器中输入31%和29%的波动率数值,计算后:
- 波动率=31%时
通过Vega估算:
看涨期权:12.8216 + 0.3897 = 13.2113
看跌期权:10.8414 + 0.3897 = 11.2311
显然我们通过Vega估算的结果和期权价值非常接近。
- 波动率= 29%时
通过Vega估算:
看涨期权:12.8216 - 0.3897 =12.4319
看跌期权:10.8414 - 0.3897 = 10.4517
同样,估算结果通过验证。
很多初学者经常忽视Vega,将期权或期权策略交易作为方向型交易方法,这在市场波动率大幅异动时会带来很大挑战。研究Vega,研究波动率,会为投资者提供更加灵活多样的交易优势。
波动率的特性
研究Vega特性离不开波动率,因此熟悉一些波动率的既有规律,对理解Vega特性及合理设计波动率交易有很大帮助。通常股票波动率会显示如下规律:
- 波动率与股票价格的高度负相关性
- 即当股票价格下跌时,波动率大幅上升
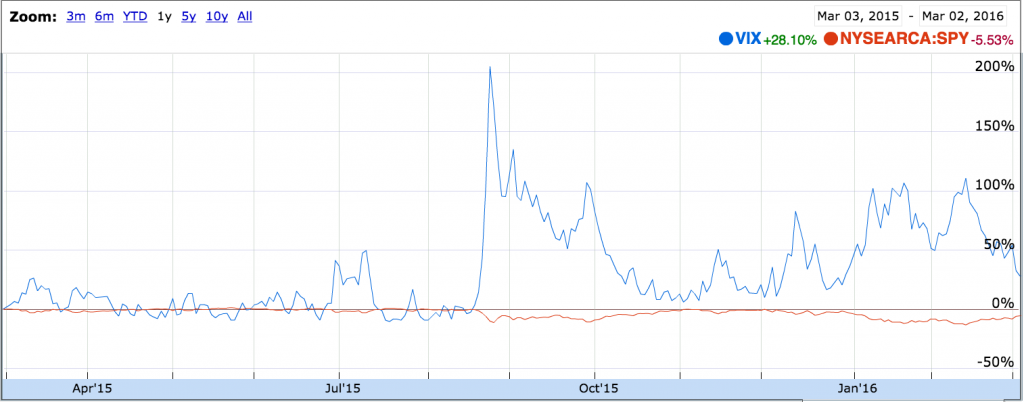
- 下图为S&P500 ETF (SPY) 相对于S&P500波动率指数(VIX)的Google Finance截图。波动率和标的价格的负相关非常明显。
- 波动率经常以群簇的方式出现
- 即波动率多数情况处于较低的水平,但高波动率出现的频率和幅度会集中在某些时间段。
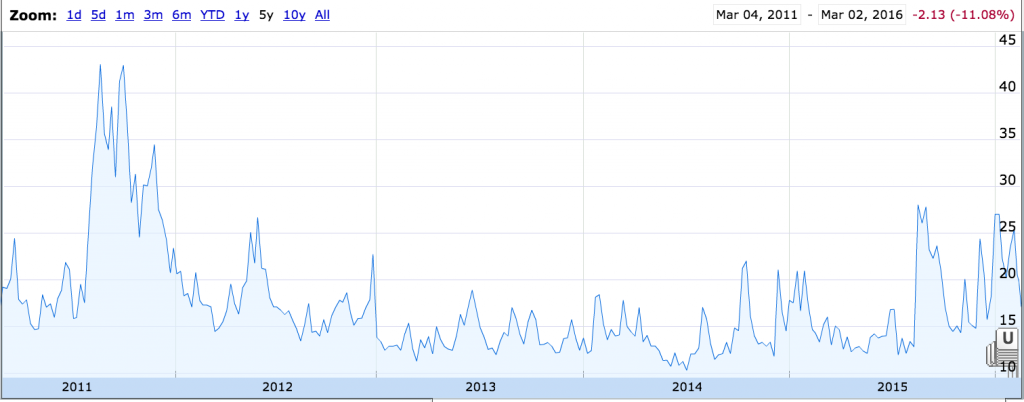
- 例如下面Google Finance的5年VIX图中的群簇效应比较明显。
- 波动率具有长期均值回归的特性
- 从上图我们还可以看出,波动率变化并没有长期方向型趋势,在大幅升高之后,通常会回落到历史长期均值
- 此外对于股票(ETF除外),波动率还经常出现周期性的规律,例如:
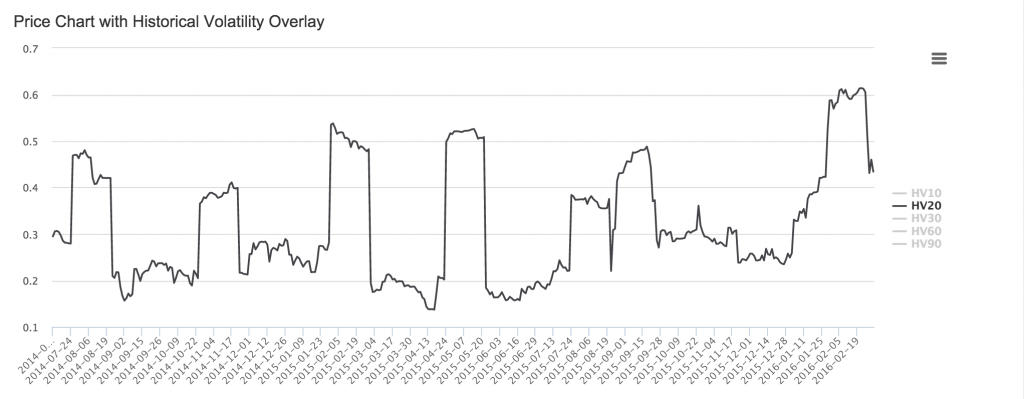
- 某些股票在季报前会出现波动率大幅飙升,季报公布后又大幅回落
- 例如如下图(权翼历史波动率与收益形态分析)显示,Amazon体现比较明显的季节性规律
Vega的特性
- 看涨、看跌期权Vega相同
前面练习计算器使用时,读者应该已经意识到,看涨、看跌期权的Vega值是一致的。
- 期权Vega总是为正
- 波动率增加时,期权价值增加,因此不论看涨、看跌期权,Vega总为正值
- 因此买入期权获得Vega多头,卖出期权活动Vega空头
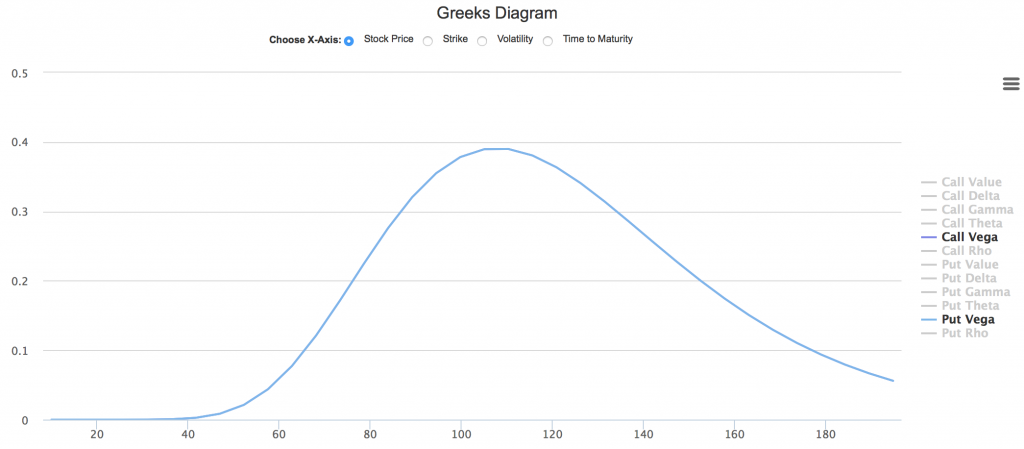
- Vega在平值附近最高
用我们的希腊字母动态图,我们可以清晰看到Vega相对于股票价格的变化规律。
显然,Vega在平值附近达到峰值。因此作为波动率交易其中一种的跨式交易,就是选择同时买入或卖出平值附近的看涨与看跌期权,期待波动率的大幅上升或下降,为策略带来收益。
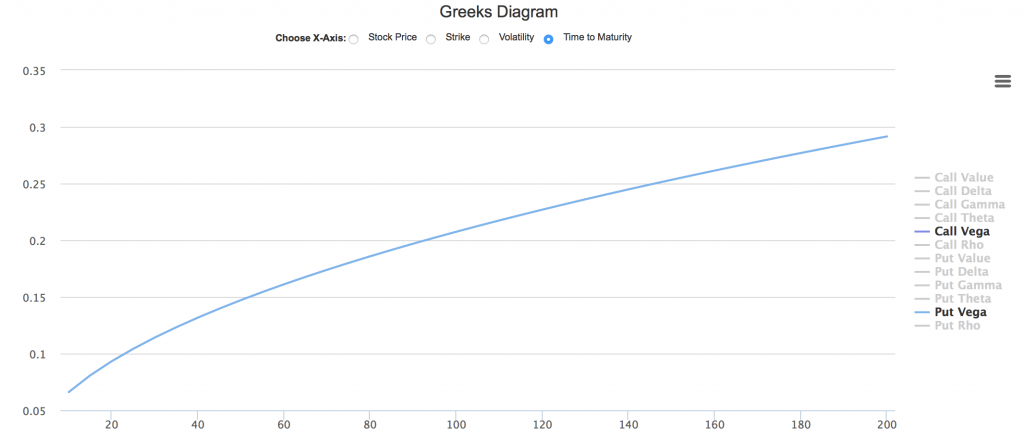
- 随着到期日的临近,Vega呈下降趋势
继续使用我们的希腊字母动态图,横坐标选择距到期日时间(Time to Maturity),我们可以看到Vega的明显下降曲线。
这一点和我们的常识比较接近,时间越短,波动率对到期日股票价格分布形态的影响就越小,因而对期权价格的影响就越小。
Vega与波动率的实用意义
Vega特性与波动率研究是密切相关的。在很多高级期权交易中,就是围绕波动率构建交易策略,通过波动率的变化,获得收益。
在前面讲解中,我们经常重复,期权交易就是波动率交易。买入期权,就是买入波动率,卖出期权,就是卖出波动率。我们知道,期权价格受期权在到期日成为实值期权的概率决定,而概率是基于到期日股票价格的形态分布计算得出。股票价格的波动率是影响到期日股票价格形态分布的关键因素。因此,波动率直接影响着期权交易的损益。事实上,对于一个使用Delta对冲实现市场中性的期权策略,最终的交易损益取决于到期日股票价格实现的历史波动率和交易建立时的隐含波动率间的差值。我们会在将来的高级期权知识中,为读者实例推导这个损益实现过程。
根据前文介绍的Vega特性与波动率规律,投资者可以构建针对波动率的交易策略。例如,读者可以在下面链接的策略分析模版中,通过调节情景模拟变量,练习使用技巧:
此外,在很多金融机构中,还有专门设计的场外交易产品,例如波动率互换协议,其交易的损益只与波动率变化相关。
权翼的核心研发围绕历史波动率的测量,未来波动率的预测,已及隐含波动率的分析进行策略与交易量化分析。希望以工具+数据的方式,为期权投资者提供优异的交易机会与交易优势。
希腊字母总结
前面几节,我们通过期权计算器和希腊字母动态图,为大家介绍了几个比较重要的风险系数。希望大家可以加强训练,在练习中体会特性与规律。期权交易不同于股票交易,使用得当,不仅灵活方便,而且进退有度。风险是收益的源头,深入理解风险是获得稳固收益的必要条件。这一点对期权交易尤为重要:
- 把握风险,把握收益
- 洞悉风险,开发交易优势