儿子的 Physics Lab Report

儿子按老师的要求把他一个物理的Lab Report Emai 给了我。我也是学工的，以前物理还不错，感觉看了还蛮费劲的。留一份作纪念。过十年让儿子自己读，看看他那时会不会觉得费劲。

Dear Mom,

 

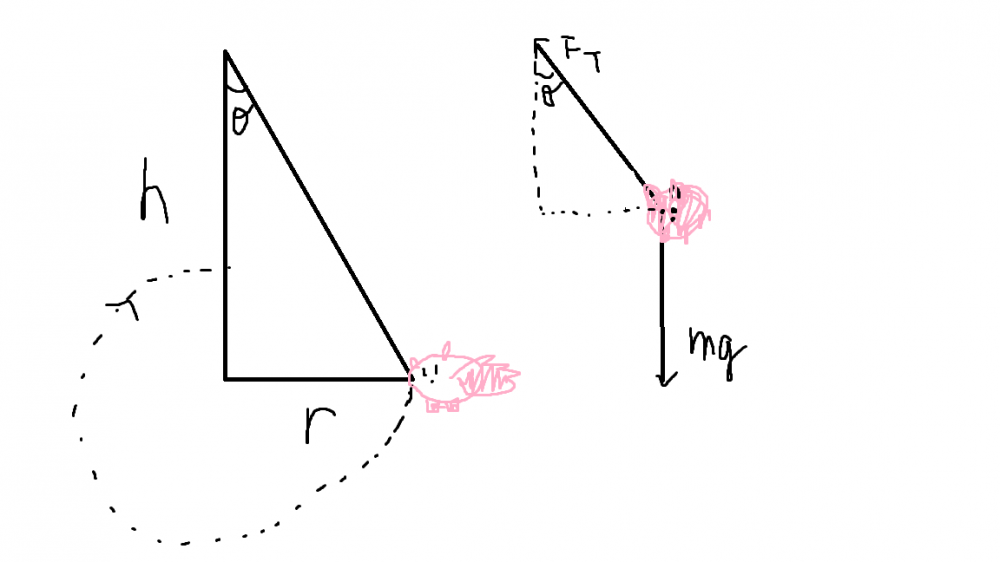
Recently in my AP Physics 1 class, we completed a lab in which a toy pig was attached to the roof by a string and was moving in a circle (see pictures). Our purpose in the lab was to predict and then calculate the velocity and acceleration of the pig. 

 

To do so, we would need to find some values. 

First, we found the vertical distance from the ceiling to the center of the pig (its center of mass) to be 104.5 cm (1.045 m). Then, we found the length of the radius at which the pig would fly with to be 49.5 cm (.495 m). Using some high school trigonometry (hope you remember how to do this), we found the angle from the ceiling at which the pig would be suspended at. Because tan(θ) = opposite/adjacent, tan(θ)=49.5/104.5. Finding θ is as simple as then taking the inverse tangent, tan^-1(49.5/104.5) = 25.34. Therefore, the angle between the point suspending the pig from the roof and the pig is 25.34 degrees.

 

Now, we need to identify all the forces that act on the suspended pig. When the pig is suspended, the force of gravity and the force of tension in the string attaching the pig to the ceiling are acting on the pig. When the pig is suspended at an angle (see diagram), the force of tension is can be broken down into its x and y components. Using trigonometry again, we see that the force of tension acting in the x-direction is equal to Ftsin(θ) and that the force of tension acting in the y-direction is equal to Ftcos(θ). Knowing this, we can write a few equations. The sum of all forces in the x-direction is simply just the force of tension in the x-direction, which is Ftcos(θ)using trig (see diagram). When objects are in circular motion, they accelerate towards the center of the circle that they revolve in. Knowing this, we equate Ftsin(θ) = mv^2/r. The sum of all forces in the y-direction is equal to the force of tension in the y-direction pulling upwards getting subtracted by the force of gravity. However, because the pig is not moving up or down, the two are equal. We can relate this by Fcos(θ)-mg=0. From this second equation, Ftsin(θ)=mg, which tells us Ft=mg/sin(θ). We can substitute this expression for Ft in the first equation, giving us mgsin(θ)/cos(θ) = mv^2/r. Dividing both sides by the mass m, we are left with gsin(θ)/cos(θ) = v^2/r. Now, we multiply both sides by the radius r to get rgsin(θ)/cos(θ) = v^2. Finally, taking the square root of both sides, we are left with an expression for the velocity v, which is dependent on only the angle the pig is suspended at and the radius (g is a constant number, 9.8). This final expression is v=sqrt(rgsin(θ)/cos(θ). We can substitute the values we found above to find the theoretical velocity of the pig. We know θ=25.34, r=.495m, and g=9.8, therefore the theoretical velocity is 1.52 m/s.  Because the pig is moving in a uniform circle, we know v^2/r = a. Because the acceleration of an object in uniform circular motion points towards the center of the circle it travels in, we find that the theoretical centripetal (center-seeking acceleration) is 4.68 m/s^2.

 

Finally, we can find our experimental velocity and acceleration. We know that the distance the pig travels is equal to the circumference of the circle it travels in. Finding the circumference, which is equal to 2pi(r), we find that the distance the pig travels is 3.11m. Knowing that distance=rate x time, rate=distance/time, where the rate is the velocity. Taking 5 trials and averaging them, we find that each lap takes 1.92 seconds to complete. Therefore the experimental average velocity of the pig = 3.11/1.92 = 1.62 m/s. Because the pig is moving in a uniform circle, we know v^2/r = a.Because the acceleration of an object in uniform circular motion points towards the center of the circle it travels in, we find that the centripetal (center-seeking acceleration) is 5.32 m/s^2.

 

Comparing these values with our theoretical, we find that our velocity has a ((1.62-1.52)/1.52))(100) = 6.6% error and our centripetal acceleration has a ((5.32-4.68)/4.68))(100) = 13.7% error. We can likely attribute this error to the pig not being in perfect uniform circular motion, making the theoretical velocity slightly off.

 

From this lab, we can conclude that we can accurately predict the velocity and acceleration of an object in uniform circular motion. We discovered that an object in uniform circular motion has its acceleration directed inwards.

 

I hope my explanation has been clear and easy to understand,