2016年诺贝尔物理学奖颁给了David J. Thouless (华盛顿大学)、F. Duncan M. Haldane(普林斯顿)、J. Michael Kosterlitz (布朗大学)三人。93万美金奖金一半给了 Thouless,另一半则是后两人分享。诺贝尔奖金数量取决于诺贝尔基金当年的收入。几年前是1000万瑞典克朗,现在降到了800万。这三位诺奖获得者的贡献是把拓扑学运用于凝聚态物理。其中的 Thouless 用拓扑学解释了整数量子霍尔效应,相关的方法被扩展到其他问题上,发现了很多奇特并且可能有极大应用前景的物理现象。相关的介绍文章很多,我就不重复了。这里稍微介绍下拓扑与物理的关系(凝聚态物理中充斥着各种人名命名的概念,我这里尽量少用术语)。
在量子霍尔效应中,霍尔电阻精确等于普朗克常数除以电子电荷的平方,准确到几十亿分之一。这个极其精确的电阻数字与样本大小、磁场大小、样本形状、样本的属性都没有关系,样本粗糙、有一定的杂质效果甚至更好。这个颠扑不破的惊人精确度与实验条件的随意性困扰了物理学相当长时间。Thouless 用拓扑不变性从理论上解释了这个问题。
诺贝尔委员会在介绍其成果时图片如下,这可不是给与会人员发点心吃。
上图是两个食品有个基本的区别,一个有两个孔,另一个只有一个。这两个东西无论怎么变形(但不能撕裂),其孔的数量 g 是不变的。这在数学里叫做拓扑不变量。欧拉在很久以前发现,任意一个多面体的顶点数量 V,边的数量 E,面的数量 F 有这个关系 V - E + F =2 。比如说一个立方面,有八个顶点 V=8,12 条边,6个 面, 8-12+6=2。你可以试试其他的多面体,都满足这个关系。一个球面可以看成有两个顶点,一个边,一个面,2-1+1=2 (试试看)。如果是有 g 个孔的,那么 V -E -F = 2- 2 g 。如下图,有一个孔 V - E + F = 2- 2*1=0。有兴趣的可以自己数数。读者可能问,这有什么特别吗? 特别的地方在于,无论把这个怎么变形,这个数字只取决于孔的数量。比如说,你可以把下面这个六角环变成一个圆环的玉镯形状 (Torus),一个顶点,两个边,一个面 , 1-2+1=0.
现在我们考虑另一个问题,如果我们在操场上围着一个圆心跑一圈、回到出发点,我们绕了360度(2 pi);但如果我们不是走圆形路径,而是走一条弯路,最后回到出发点,那么我们绕圆心转了多少度呢?不管你是怎么绕的,绕一圈就是360度,绕两圈总共是720度。不管你如何走弯路,你可以把走的路分成很多小段,把每一段绕圆心变化的角度加起来,变成一个积分,结果肯定是 360度的整数倍,倍数是转圈的数量。路径变形(但保持圆心在路径内),这个圈数不变。我们说,这个圈数是一个拓扑不变量。
类似的,围绕一个球心的球面角度是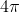 .如果把球面变形,这个角度也是这个数字。对于有 g 个孔的情况,高斯有个普遍公式,对于一个光滑而且没有边界的面,曲率乘以面积的积分等于 4 PI 乘以 1-g.
.如果把球面变形,这个角度也是这个数字。对于有 g 个孔的情况,高斯有个普遍公式,对于一个光滑而且没有边界的面,曲率乘以面积的积分等于 4 PI 乘以 1-g.
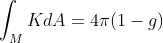
对于半径为r的球面,没有孔 (g=0),曲率等于 1/r^2, 面积为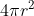 ,我们很容易验证结果正确。如果是圆环,有一个孔,结果是0 -- 圆环内侧的曲率是负值,结果跟外侧的抵消了。这个公式的“神奇”在于,左边是几何曲率的积分,右边却是一个拓扑属性,不管怎么变形,右边都是固定的。这就把整体的几何属性跟拓扑结构联系起来了。
,我们很容易验证结果正确。如果是圆环,有一个孔,结果是0 -- 圆环内侧的曲率是负值,结果跟外侧的抵消了。这个公式的“神奇”在于,左边是几何曲率的积分,右边却是一个拓扑属性,不管怎么变形,右边都是固定的。这就把整体的几何属性跟拓扑结构联系起来了。
拓扑可以解释物理中某些基本而又困难的问题。我们知道,电荷总是电子电荷的整数倍 (夸克电荷可以是1/3,但夸克不能自由存在),从未发现过0.12个电荷之类。这个电荷的整数特性被称为电荷的量子化。为了解释这一点,DIRAC 假设存在磁单极子,然后考虑电荷绕圈,那么从角动量的量子化就可以推导出电荷的量子化。可以说,DIRAC 这个电荷量子化的解释是拓扑的。问题是,到目前为止,并没有发现磁单极子,而且我们也没有另一种电荷量子化的解释 --- 尽管这是一个明摆着的事实。
对于一个与某些参数相关的量子系统,如果这些参数沿着某个路径缓慢变化,但最终回到开始的值,这个量子系统会回到原来的状态。但是量子波函数可能出现一个相角的变化。如果计算这个角度的总变化,是一个环路积分。可以证明,这个相位的变化与路径有关但与动态过程无关,是一种“几何”性质。但我们知道,环路积分可以跟环内的面积分对应(这叫着斯托克斯定理)。如果我们考虑反向路径的积分,那么应该跟外围的面积分对应。反转与顺转的结果应该抵消,但是相角的总变化可以是 2 PI 的整数倍。因此,整个面积分应该是 2PI 的整数倍。相关的复数理论之前已经被陈省身发展出来,这个整数叫着陈数(Chern number)。
Thouless 正是利用了这样的数学解释了量子霍尔效应。他从线性响应出发推导出霍尔电导的方程,并证明了霍尔电导只与 K 空间的拓扑属性有关。(此处省略N字。。。)这被称为 TKNN 不变量,其中T指 Thouless (点击查阅这个姓氏的起源)。也就说明了为什么量子霍尔电导的精确度是如此的坚实、可靠,不受干扰。
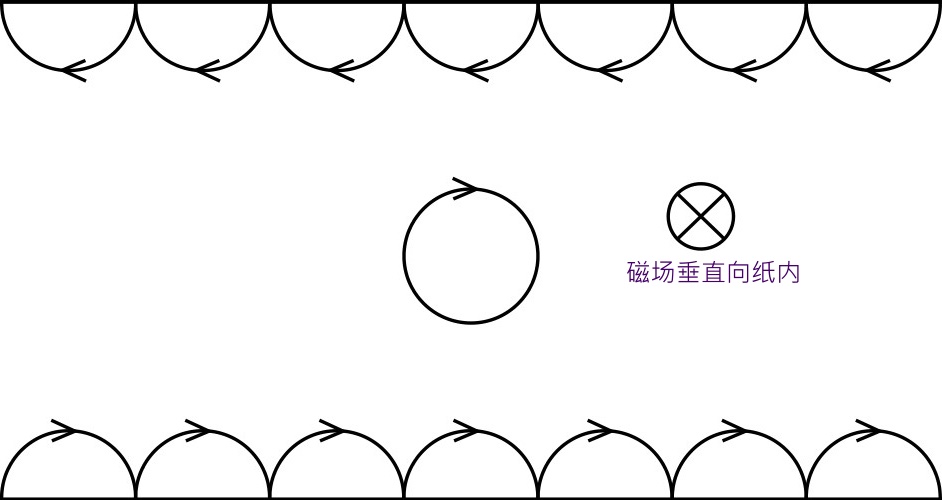
也许用半经典的模型更好理解。下图中,磁场垂直向纸内,由于电子带负电,根据右手法则,从左向右运动的电子会受到向下的力,从右向左运动的电子会受到向上的力。在磁场足够强时,中间的电子会做顺时针的圆周运动,不参与导电,这叫拓扑绝缘体。在下边的边缘处,电子向右运动半个圈就会遇到边缘势垒反弹回来;但由于磁场的存在,反弹的电子即使是遇到障碍,也不会从左边出去,而是顺时针绕回去继续向右前进。类似的,上面边缘处的电子只能向左运动,无法反弹转向。这就把向左运动与向右运动的通道隔离了。由于两个边缘的距离远大于中间圆轨道的半径,一个在下面向右运动的电子要跑到上面转向成向左的几率极小,因此上下两个通道的电子输运完全是没有反射的,或者说传输效率为100%。在一维量子输运中,我们知道理想情况的电导是 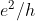 (这叫做 Landauer 公式)。这个情况跟一维理想的 ballistic 输运非常类似,只是这里电压是加在垂直于电流的方向,导致的是霍尔电导 Ix/Vy。
(这叫做 Landauer 公式)。这个情况跟一维理想的 ballistic 输运非常类似,只是这里电压是加在垂直于电流的方向,导致的是霍尔电导 Ix/Vy。
由此可见,量子霍尔效应中磁场的作用是把左右两个边缘通道从空间上分开了。用现在流行的行话来说,形成了两个方向的 chiral state,破坏了time reversal symmetry,云云。如果没有磁场,但能把左右运动的两个通道完全分开,也应该有类似的量子霍尔效应。这种直观的模型似乎更加容易解释相关的物理。

.如果把球面变形,这个角度也是这个数字。对于有 g 个孔的情况,高斯有个普遍公式,对于一个光滑而且没有边界的面,曲率乘以面积的积分等于 4 PI 乘以 1-g.
,我们很容易验证结果正确。如果是圆环,有一个孔,结果是0 -- 圆环内侧的曲率是负值,结果跟外侧的抵消了。这个公式的“神奇”在于,左边是几何曲率的积分,右边却是一个拓扑属性,不管怎么变形,右边都是固定的。这就把整体的几何属性跟拓扑结构联系起来了。