慕容青草的博客
哲学园地戴榕菁
之所以反复谈相对论质量,相对论动量和相对论能量这几个量是因为它们不但对于我已完成的推翻狭义相对论的工作很重要而且对于认识量子场论的逻辑缺陷极为重要。所谓的相对论质量(也被称为动质量)指的是:
M=γm (1)
所谓的相对论动量指的是:
P = γmv (2)
所谓的相对论能量(也被称为相对论总能量)指的是:
E = γmc2 (3)
其中m是粒子的质量(也被称为静质量),v是粒子运动速度,γ是所谓的洛伦兹因子,由下式给出:
γ = 1/√(1-v2/c2) (4)
1. 相对论质量
去年年底我已提到当今物理学界的主流已普遍不承认相对论质量【[1],[2],[3]】。今年初我在“相对论质量的一笔糊涂账”一文中又提到有报道说1948年爱因斯坦曾私下里否认相对论质量的意义尽管公开地他仍为鼓吹相对论质量的作者站台。
虽然据说是洛伦兹最早提出相对论质量这个概念的,但如同洛伦兹变换一样,爱因斯坦1905年在他的被认为后人认为是狭义相对论宣言的“On the Electrodynamics of Moving Bodies” 【[4]】一文中又正式地以数学公式定义了相对论质量。只不过他在那里的定义同时也正确地暴露出相对论质量概念的逻辑缺陷从而为日后人们普遍否认相对论质量埋下了种子。在那篇文章中,爱因斯坦定义了不同方向的相对论质量:
纵向质量
 (5)
(5)
横向质量
 (6)
(6)
这种各向异性的质量的最大问题显然是与后来爱因斯坦自己为广义相对论提出的引力质量与惯性质量等效的原理相矛盾,因为一个物体只有一个引力质量。实际上,今天物理学界之所以普遍不承认相对论质量应该不仅是因为上面的各向异性,更重要地,如我在【1,2,3】中指出的,应该是他们从未在实验室里测出过远大于静止质量的相对论质量。
虽然在加速器中测量粒子的质量不是一件容易的事情,但如果接近光速运动粒子的质量会发生如(1)或(5,6)式所预言的巨大变化的话,我们仍应该能在实验室中观察到该效应。我们知道在重力场中进行水平运动的物体的路径会因为重力作用而呈现抛物线型。因此,当一个被加速到接近光速的粒子在加速器中运行了几万圈之后,如果它的质量如(1)或(5,6)式所预言的那样成倍地增长,那么它所走的抛物线应该与质量没有变化的粒子的有可被观察到的明显不同。所以,今天的主流物理学界之所以普遍不承认相对论质量,应该是他们从未观察到这样的不同。
就连极力吹捧包括相对论动量在内的各种狭义相对论概念的费米实验室的林肯博士也专门做了一集视频否认了相对论质量的意义【[5]】。不过,他没有认识到的一点是:他在那个视频中极力鼓吹的相对论动量根本就不是动量,而是一个作为空中楼阁的数学定义,与经典的动量之间并没有直接的逻辑关联。
2. 相对论动量和相对论能量
如我在“几点重大补充说明和结论”一文中指出的,爱因斯坦在1905年的“On the Electrodynamics of Moving Bodies” 【4】中推导出了电场中运动的单一带电粒子的动能:
W = mc2{γ-1} (7)
又在1905年的另一篇著名文章“Does the Inertia of a Body Depend Upon Its Energy-content?”【[6]】中推导出了质量-能量关系:
E = mc2 (8)
尽管他在推导(7)式时还没有得出(8)式样,但他在文章【6】中仍然可以将(7)式和(8)式相加得出(3)式,但他没有这样做。这里的主要原因应该是他认为(8)式才是总能量,另外他已在文章【4】中的表明了相对论质量是各向异性的,而(3)式不能反映这一点。
2.1. 相对论动量-能量关系
其实,如果作为相对论质量的(1)式是正确的,那么顺理成章地我们就可以定义相对论动量和相对论总能量为:
P = Mv (9)
E = Mc2 (10)
将(1)代入(9)和(10)我们就可以得到(2)和(3)。这应该就是历史上人们最初得出相对论动量和能量的逻辑,而这么做的前提是相对论质量不能是爱因斯坦在文章【4】中给出的(5)和(6)式,而必须是(1)式那样的各向同性的单一标量。
有了(2)和(3)后,由(2)式平方得:
p2 = m2v2c2/(c2-v2) (11)
由(3)式平方得:
E2=m2c4 + c2(m2v2c2/(c2-v2)) (12)
由(11)和(12)得:
E2=p2c2+m2c4 (13)
这就是作为量子场论的基础的著名的相对论动量-能量关系。
3. 量子场论的逻辑缺陷
我在“抢救量子大兵---狄拉克方程不属于狭义相对论”和“几点重大补充说明和结论”中指出狄拉克方程不会因为狭义相对论被推翻而被否定。但狄拉克当初自己是实实在在地认为他是按照狭义相对论来推导出他的方程的【[7]】(见附录)。狄拉克在推导中是按照之前的Klein-Gordon的思路选了一个哈密尔顿函数,而那个函数在本质上就是将(13)式的左边移到右边去再加上势能。
但是,当我们从上面的讨论中了解了(13)式及推出(13)式所谓的相对论动量和相对论能量的(2)和(3)式来历之后,更重要的是当了解了得出(2)和(3)式的相对论质量(1)的先天的逻辑缺陷之后,我们会很自然地看到(13)式所存在的先天的逻辑缺陷:
从本质上来说,狄拉克的可以得出今天被认为是他对量子论最重要的两个贡献(确定电子存在相反自旋和正电子的存在)的方程是从两个人为定义的与动量和总能量并没有严格的逻辑关系(因而不受经验逻辑的支持)但被称之为动量和总能量的公式(2)和(3)出发得出公式(13),然后通过相关的构造(即选用已知的泡利旋转矩阵及量子化)来得出的方程。。。。由这样的方程得出了上述两个重要的量子论结论,而且这两个量子论的结论看来已经定性地得到了实验的证实。这不得不说是20世纪物理学的诸多奇幻现象中一个!
翻译成更通俗易懂的大白话就是这样的:20世纪的物理学界人为地定义了两个公式(2)和(3)并称它们为相对论动量和相对论总能量。从这两个人为定义的公式出发可以得到公式(13),然后地奇幻地从(13)出发引入泡利大师的三个自旋矩阵后推出了作为量子场论基础的被认为是20世纪最伟大的物理成就的狄拉克公式。而由这个公式出发,人们得出了关于电子的两个极为重要的结论:一个原子轨道上可以有两个自旋相反的电子以及存在着电子的反粒子,即正电子。------魔术般的奇妙!
当我们去阅读狄拉克的文章【7】时会发现,狄拉克在推导出方程的过程中除了(13)式(即他的哈密尔顿)之外并没有再用到能量守恒和动量守恒,因此除了那个作为出发点的(13)式是一个在逻辑上没有经验基础的空中楼阁之外,倒也没有直接违背能量守恒或动量守恒。不过,狄拉克在推导出他的方程后,运用他的方程求解的过程中用到了动量守恒,而他所用的动量就是(2)式定义的量,因此,从原则上说他在那里就因为对不属于动量的数学表达式(2)应用动量守恒而额外地引入了逻辑错误。但奇妙的事再次发生:他的求解不涉及碰撞或裂变,而所求的电子的运动速度被认为(基本)不变,在这个前提下动量守恒(基本上)是可以用在由(2)式定义的数学表达式的。因此,狄拉克又(基本上)安全过了一关。
而他之后再运用总能量守恒从原则上来说问题就有点大,但是他所针对的只是单一带电粒子在有电磁场的真空中的运动,那么我在“抢救量子大兵---狄拉克方程不属于狭义相对论”和“几点重大补充说明和结论”中提到的海维赛德椭球体又为他解了围。
所以,狄拉克方程最奇幻之处还在于从一个本身并不具备严格的物理意义的(13)式出发,得出了具有物理意义的两个重要结论。
当然,我们也不能说(13)完全没有一点物理意义。比如,如我在本文前面及“几点重大补充说明和结论”一文中指出的,我们可以从上面的公式(7)和(8)推出(3)式来,当然这里还需要用海维赛德椭球体来为洛伦兹变换解套。只不过爱因斯坦在推出(7)式时要求了一个前提条件的,那就是电子运动速度不快因而它不向外辐射能量或辐射能量可以被忽略。但另一方面,对于狄拉克所针对的氢原子轨道上运动的电子来说,虽然被认为速度接近光速,但是却不向外辐射能量(否则这个世界就没有稳定的原子了)。所以,虽然狄拉克的电子速度很快,却满足爱因斯坦推导(7)式的前提条件。所以,对于狄拉克的电子来说,用于推导出(13)式的(3)可以被认为具有能量的意义。但如我之前反复指出过的,(2)式肯定不具备动量的意义,因为当速度等于0时,(2)也归于0,它永远也不可能回归到经典的动量mv。
不管怎么说,用一个只在非常有限的范围内具有能量意义的(3)式和任意定义的(2)得出(13)式,然后从(13)式出发得出对于量子论来说最重要的两个结论是20世纪物理学之奇幻的重大表现!。。。。。。
附录. 狄拉克方程推导过程的思路
首先,他选了一个哈密尔顿函数:
 (14)
(14)
其中A0和A是电磁场的势能,e是电荷,p是动量,W应该就是经典的哈密尔顿。应该说狄拉克对于哈密尔顿函数的选择与物理学界其他人一样表现的很随意,不严格。我这么说的原因是如我之前提到过的,哈密尔顿和拉格朗日力学的基本依据是没有人能明确说出为什么的最小作用原理。但在经典力学和光学中,最小作用原理和牛顿力学及几何光学非常一致。到了量子论和相对论,物理学家们就模仿经典力学但相当随心所欲地选取对应着最小作用原理的拉格朗日或哈密尔顿函数。这里的一个比较明显的潜在危机是最小作用原理似乎对能量守恒有较高的要求,但量子场论的虚拟粒子并不总能满足这一条件。
不管怎么说,(14)式在本质上就是将(13)式两边除以c2,并将的E2/c2移到右边,然后令哈密尔顿函数F = -E2/c2 + p2 + m2c2,并加上电场势能和磁场势能的影响。狄拉克对(14)做了如下的量子化(quantization)的操作:
 (15)
(15)
并令量子化后的哈密尔顿函数为零(经典的量子化操作)从而得到:
 (16)
(16)
(16)式就是文章【7】里的(1)式。他略去电磁场势能后得到:
 (17)
(17)
其中的

(17)式就是文章【7】中的(3)式,它与我们直接将(13)式除以c2之后再进行量子化的结果除了表达符号不同之外完全一样了。
在“抢救量子大兵---狄拉克方程不属于狭义相对论”和“几点重大补充说明和结论”文中我都提到了将(13)进行因式分解,那是后来的物理学者们采取的方式。其实,狄拉克的原文中搞得没有这么干净爽快。他先是做了一个线性假设,声称相对论要求p0, p1, p2, p3都是对称的,所以哈密尔顿函数必须是线性的,所以(17)可以降阶为:
 (18)
(18)
其中α1,α2,α3,和β独立于p0, p1, p2, p3。(18)式是文中【7】的(4)式。接下来他又做了一个假设:他说由于这里考虑的是粒子在真空中运动,所以哈密尔顿函数不应该含有t, x1, x2, x3,所以α1,α2,α3,和β也独立于t, x1, x2, x3。根据这一点他认为我们应该可以将(18)式扩展为:
 (19)
(19)
这是文章【7】的(5)式。
从上面(17)到(19)的操作我们可以看出,狄拉克很奇怪地把原本可以一步进行的因式分解化作两步:先用一个线性假设将(17)降幂为(18),再用一个线性假设将(18)升幂为(19)。
狄拉克在将(17)变为(19)的过程中提出了两个线性假设,它们对于因式分解来说是不需要的,因为将(13)直接进行因式分解其实严格来说并不需要线性假设的,因此狄拉克的这两个线性假设是为他接下来的推导所做的假设而已。
将(19)展开之后与(17)对比,我们可以得到:
 (20)
(20)
狄拉克进一步将β取值为:
 (21)
(21)
则上面的关系变为:
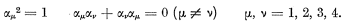 (22)
(22)
(22)是文章【7】中的(6)式。接下来他做了一个逆向逻辑操作,这一操作使得他的推导完全就不是一般的逻辑推导,而是一种构造。而他之所以进行这种构造的原因很显然是因为他事先已经知道了泡利大师的旋转矩阵所具有的特性。他首先选取泡利大师的下面这三个著名的旋转矩阵:
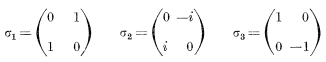 (23)
(23)
这三个矩阵满足下式:
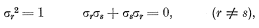 (24)
(24)
于是狄拉克打马虎眼地声称(24)和(22)是一样的。当然,这里他打了马虎眼,因为(22)是单纯数值之间的关系而(24)是矩阵之间的关系。(24)中的1不是数值1,而是单位矩阵。接下来他将泡利矩阵进行扩展:
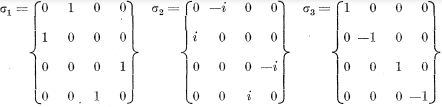 (25)
(25)
并按照上面三个矩阵另造三个:
 (26)
(26)
他接着又再打马虎眼,令:α1=ρ1σ1, α2=ρ1σ2, α3=ρ1σ3,。这里的马虎眼比较大,因为他将前面用来表示单纯数值的α1, α2, α3转身一变成为了矩阵,而且是4阶矩阵。狄拉克接着指出它们满足和(22)一样的关系:
 (27)
(27)
然后他将经过改头换面的α1, α2, α3 和β 代入(18)式,便得到:
 (28)
(28)
其中的σ代表的是(σ1, σ2, σ3)。(28)式是文章【7】中的(9)式,它就是著名的狄拉克方程的最原始的形式。
到这一步为止,狄拉克既没有涉及到电子的任何特性,甚至也没有涉及到洛伦兹变换或任何狭义相对论的要素,这使得狄拉克感到有必要在得出(28)式之后马上在文章【7】的§ 3. Proof of Invariance under a Transformation.来证明(28)式符合洛伦兹变换。不过,这一步多少有点奇怪,难得狄拉克真的就只是如他的文章中叙述的那样只是按照前人的习惯来选取了一个哈密尔顿函数而没有意识到他的那个哈密尔顿函数的依据是本文前面的由相对论能量和动量关系得出的(13)式???但另一方面,他的证明也表明了由他的哈密尔顿(即13式)得出的结果一定满足洛伦兹变换,因而一定只在非常局限的范围(如单一电子不涉及碰撞或裂变)的情况下成立。
在证明了(28)式符合洛伦兹变换之后,狄拉克才在文章【7】的§ 4. The Hamiltonian for an Arbitrary Field 中重新引入电磁场势能从而开始讨论与电子有关的议题。在这一节里他得出了电子的他称为“貌似”旋转的力矩表达式。
然后在§ 5. The Angular Momentum Integrals for Motion a Central Field.狄拉克开始讨论环绕中心运动的电子,也就是氢原子轨道上的电子的角动量守恒。在这推导过程中首先他强调只是周期运动,其次这过程中没有涉及到他所谓的动量的导数,因此,即便由他的哈密尔顿函数得出的动量一定是前面的(2)式定义的表达式,它也同样满足守恒方程。在这一节中他得出电子正反自旋(正负)h/2的形式。
在§ 6. The Energy Levels for Motion in a Central Field中狄拉克开始讨论环绕中心力运动的电子的能级问题。
这里我可以看出:所谓的狄拉克方程预言了原子轨道上可以有自旋相反的电子是因为狄拉克人为地在他的方程中引入了泡利大师用来表达旋转的矩阵,而不是直接推导出了的。而他能得出电子的反粒子即正电子存在的结论是因为(19)式中包含了能量值(或质量值)的正负号相反的两个方程。
当然,我们也不能因为上述的方程是构造出来的而且是逆阶构造出来的而否认它是推导出的,毕竟我们可以将(28)拆为16个非矩阵的方程,每个方程又都是和(17)式(也就是13式)一样。
这里最随机的一步其实就是他选择那个哈密尔顿函数。由我们在前面对(13)式的来历的讨论中可知,(13)中的所谓动量只是一个被称为动量但实际并非动量的数学表达式,而其中的能量也只在非常有限的范围内真正具有能量的意义。这就决定了狄拉克的哈密尔顿函数肯定不会在一般的情况下满足最小作用原理所苛求的能量守恒。不过,如前面讨论的,在狄拉克所针对的真空(带有或不带有电磁场)中运动的单一带电粒子来说,他所选的哈密尔顿函数中的能量具有实际意义,另外,虽然其中的所谓动量只是一个数学表达式而已,但满足(13)式,只是用它进行的动量守恒的计算一定有误差。
[[1]] 戴榕菁 (2022)“砍错对象了。。。。真正更可怕的是。。。。?”
[[2]] Dai, R. (2022). “E = mc^2 is not the total energy”. Retrieved from: https://wp.me/p9pbU7-fa
[[3]] Dai, R. (2022). “The Real Meaning of E=mc2”. Retrieved from: https://wp.me/p9pbU7-fO
[[4]] Einstein A. (1905) “On the Electrodynamics of Moving Bodies”. Zur Elektrodynamik bewegter Körper, in Annalen der Physik. 17:891, 1905, translations by W. Perrett and G.B. Jeffery. Retrieved from: https://www.fourmilab.ch/etexts/einstein/specrel/www/
[[5]] Fermilab (2018) YouTube “Is relativistic mass real?”. https://youtu.be/LTJauaefTZM
[[6]] Einstein, A. (1905a). “Does the Inertia of a Body Depend Upon Its Energy-content?”. Retrieved from: https://www.fourmilab.ch/etexts/einstein/E_mc2/e_mc2.pdf
[[7]] Dirac, P. A. M. (1928). "The Quantum Theory of the Electron". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 117 (778): 610–624. Retrieved from: https://royalsocietypublishing.org/doi/epdf/10.1098/rspa.1928.0023





到这一步为止,狄拉克既没有涉及到电子的任何特性,甚至也没有涉及到洛伦兹变换或任何狭义相对论的要素,这使得狄拉克感到有必要在得出(28)式之后马上在文章【7】的§ 3. Proof of Invariance under a Transformation.来证明(28)式符合洛伦兹变换。不过,这一步多少有点奇怪,难得狄拉克真的就只是如他的文章中叙述的那样只是按照前人的习惯来选取了一个哈密尔顿函数而没有意识到他的那个哈密尔顿函数的依据是本文前面的由相对论能量和动量关系得出的(13)式???但另一方面,他的证明也表明了由他的哈密尔顿(即13式)得出的结果一定满足洛伦兹变换,因而一定只在非常局限的范围(如单一电子不涉及碰撞或裂变)的情况下成立。
在证明了(28)式符合洛伦兹变换之后,狄拉克才在文章【7】的§ 4. The Hamiltonian for an Arbitrary Field 中重新引入电磁场势能从而开始讨论与电子有关的议题。在这一节里他得出了电子的他称为“貌似”旋转的力矩表达式。
然后在§ 5. The Angular Momentum Integrals for Motion a Central Field.狄拉克开始讨论环绕中心运动的电子,也就是氢原子轨道上的电子的角动量守恒。在这推导过程中首先他强调只是周期运动,其次这过程中没有涉及到他所谓的动量的导数,因此,即便由他的哈密尔顿函数得出的动量一定是前面的(2)式定义的表达式,它也同样满足守恒方程。在这一节中他得出电子正反自旋(正负)h/2的形式。
在§ 6. The Energy Levels for Motion in a Central Field中狄拉克开始讨论环绕中心力运动的电子的能级问题。
这里我可以看出:所谓的狄拉克方程预言了原子轨道上可以有自旋相反的电子是因为狄拉克人为地在他的方程中引入了泡利大师用来表达旋转的矩阵,而不是直接推导出了的。而他能得出电子的反粒子即正电子存在的结论是因为(19)式中包含了能量值(或质量值)的正负号相反的两个方程。
当然,我们也不能因为上述的方程是构造出来的而且是逆阶构造出来的而否认它是推导出的,毕竟我们可以将(28)拆为16个非矩阵的方程,每个方程又都是和(17)式(也就是13式)一样。
这里最随机的一步其实就是他选择那个哈密尔顿函数。由我们在前面对(13)式的来历的讨论中可知,(13)中的所谓动量只是一个被称为动量但实际并非动量的数学表达式,而其中的能量也只在非常有限的范围内真正具有能量的意义。这就决定了狄拉克的哈密尔顿函数肯定不会在一般的情况下满足最小作用原理所苛求的能量守恒。不过,如前面讨论的,在狄拉克所针对的真空(带有或不带有电磁场)中运动的单一带电粒子来说,他所选的哈密尔顿函数中的能量具有实际意义,另外,虽然其中的所谓动量只是一个数学表达式而已,但满足(13)式,只是用它进行的动量守恒的计算一定有误差。