朱八八
深度八一八牛人们,走近大神的世界,探索自由心灵,感悟独立思想。“欧拉计算时毫不费力,就像人呼吸、或者鹰在风中保持平衡一样。”——法国物理学家阿拉果
01
巴塞尔(Basel)城是瑞士的第三大城市,它也是欧拉和伯努利家族的故乡。
欧拉的出生地被用来命名了一个著名的数论问题--巴塞尔问题,这个问题首先由皮耶特罗·门戈利在1644年提出,由于这个问题难倒了以前许多的数学家包括约翰.伯努利,牛顿和莱布尼茨等等,欧拉出马,一解成名,当时他年仅二十八岁。
巴塞尔级数题目看起来简单,就是精确计算所有平方数的倒数的和,也就是以下级数的和:
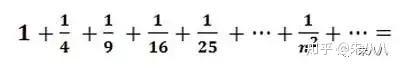
这个级数的和大约等于1.644934。巴塞尔问题就是是找到这个数的准确值,并证明它是正确的。
这道题对于那些想让孩子爬藤去名校的家长很有价值,因为它经常出现在名校如剑桥的本科数学入学考试题中。(所以下面重要的知识点务必要多看两遍。)
欧拉解题的方法巧妙和新颖得让人窒息,天才用了不到2页纸:

欧拉得到的结果很神奇,很不可思议,答案是π^2/6。所有平方数的倒数的和居然无端出现了圆周率π这个神奇的数字。这个世界冥冥之中不知道还蕴藏着多少这样的神奇。
我们以前在冯.诺依曼系列中已经很熟悉的物理学家尤金.维格纳,他在其著名文章“数学在自然科学中不合理的有效性”中讲了个笑话:
两位曾经的同班同学开始介绍各自的工作。 一位是统计学家,研究人口趋势。他给朋友看了最近的文章,文章开篇即是高斯分布。朋友很不解,指着高斯分布中的π 问道,
“这是什么?”
“这是圆周长与其直径之比。”
“你太会开玩笑了,人口怎么会和圆的周长有关系呢?”
“…”
当然,今天的我们对π出现在任何地方都很淡定了。
其实这样证明还不是很严密(欧拉后来还给出了一个严谨但复杂的证明),还需要进一步完善(牛爸牛妈看出来了吗?),但欧拉之前老老实实地计算了级数的部分和,并一口气算到了小数点后20位!他发现,级数真的趋于π^2/6,不多不少。这给了他足够的自信心,把这个结果公诸于众。
欧拉对这个结果很满意,但他没有玩够,传奇还在继续,1737年,欧拉在这个基础上接着发现了欧拉乘积公式:

等式左边就是大名鼎鼎的黎曼ζ函数。
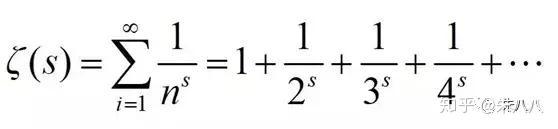
当S=2 时候的特例,就是让欧拉一战成名的巴塞尔级数。
而当S=1 时候的特例,就是著名的调和级数,欧拉研究调和级数时顺便贡献了非常有用的欧拉常数,约为0.57721566490153286060651209。 目前无人知晓欧拉常数是否为有理数。
而当S=-1 时候的特例,就是全体自然数的和, 1+2+3+4+…是多少?欧拉通过幂级数展开得出一个惊人的结论,全体自然数的和是-1/12。
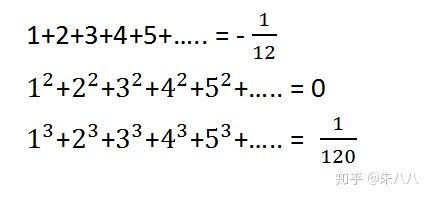
然后欧拉继续玩,而且是花式玩法,他继续算出所有自然数的平方和是0、所有自然数的立方和是1/120,答案都是匪夷所思。一年级的小学生都能一眼看出这些答案肯定“不对”。

但事实上,不论用什么方法计算1+2+3+4+…之和,只要不是无穷大,就是-1/12。
后来黎曼做了个巧妙的解析延拓,他在1859年找到了ζ函数的解析延拓,求出了ζ(-1)的值,轻易得出1+2+3+4+…和是-1/12这个结论,和欧拉的答案殊途同归。
但是直到今天,我们都不知道这意味着什么,只知道在量子力学中如果遇到全体自然数和,-1/12代替无穷就总能得到最符合实验结果的数值。
比如在弦论中,用欧拉的-1/12代替无穷大,难题立马解决,轻松得出空间维数E=10,加上一维时间,那么时空就是11维的,欧拉200多年前的怪异结论居然让弦理论重获新生。
“在数轴的无穷远处,蕴藏着崭新的数学体系等待我们建立。”……
简直世界观都要崩溃了有木有? 常识都靠不住了有木有?
如果你一定要维持你的世界观不倒的话,就拼命记住这一点:这个求和,已经不再是你小学时学过的求和了,而这里面的“等于”也不是一般的等号,而是表示某种未知的等价关系。
再啰嗦一点,这个求和是基于函数的解析延拓求和(拉马努金求和),而非一般的收敛的无限数列求和(柯西和)。
02
欧拉乘积公式发现了素数分布问题与上面这个黎曼ζ函数(ζ读音Zeta)的联系,使得黎曼ζ函数成为研究素数分布问题的经典方法。
另一个奇才,德国数学家伯尔尼哈德·黎曼大神继续欧拉的工作,并将欧拉所做的一切牢牢地置于坚石之上。他定义了黎曼ζ(Zeta)函数并在1859年提出了最著名的黎曼猜想。

更通俗的数学表达式是这样的:
令 黎曼ζ函数 =0 的所有非平凡解都在直线 x=1/2上。
这里的平凡零点是某个三角 sin 函数的周期零点;非平凡零点是ζ函数自身的零点。
也许你表示完全看不懂黎曼猜想,那太正常不过了,如果你一上来就完全明白,那只有一种可能,就是你已经花了许多时间研究过黎曼猜想是什么了。
不管怎样,黎曼猜想是数学中一个重要而又悬而未决的难题,是璀璨数学皇冠上最难采撷的明珠。
冯.诺依曼的老师,数学武林盟主希尔伯特曾说,如果他在沉睡1000年后醒来,他将问的第一个问题便是:黎曼猜想得到证明了吗?
在他著名的23问中,其中第八问黎曼猜想、哥德巴赫猜想和孪生素数问题依然是数学界一大悬案。
(朱八八注:当年陈景润证明“1+2”难题的文章在《人民文学》上发表后,哥德巴赫猜想成为中国民间科学爱好者的最爱,中国科学院每年都收到“几麻袋”的讨论或声明,号称证明了“1+1”。但是,几乎没有多少民间科学家去碰黎曼猜想,尽管其意义更加重大,而且在长期高达一百万美元的重奖之下也无勇夫。原因很简单,除了羊群效应,像黎曼猜想这种绝顶难题,民科估计连看题目都两眼一抹黑。)
2018年9 月 24 日,现年 89 岁的英国著名数学家、阿贝尔奖和菲尔兹奖得主迈克尔·阿蒂亚爵士,宣称自己已经证明了黎曼猜想。虽然目前学界普遍认为,阿蒂亚压根没有证明黎曼猜想。但英国老爷子至少又把黎曼猜想炒得火热。
有新闻说如果黎曼猜想被证实的话,将危及RSA公钥密码学的安全。“互联网都要裸奔”,还有“黎曼猜想被证明,基于 RSA 的区块链项目都将湮灭!”
目前加密货币市场上的加密货币几乎都是由哈希运算函数和数字加密证书两方面构成的。
哈希算法和素数无关。加密算法,如果是椭圆曲线数字签名,和素数分解没有特别大的关系;如果是非对称加密,实际上是在做素数分解,和黎曼猜想的找素数关系也不大。
这些媒体就喜欢蹭热点,还喜欢危言耸听,不过大家可以安心过年,黎曼猜想就算被证明,也亡不了RSA公钥密码,亡不了区块链,更亡不了互联网!
2019年1月11日迈克尔·阿蒂亚爵士去世,享年89岁,在他生命的最后一年,他还在勇战风车,挑战世界性难题,“阿蒂亚是非常单纯的人,他愿意不计较个人得失,为热爱的数学事业付出,这是很多数学家、科学家做不到的。”一位数学研究人员说,能够引起社会对数学如此的关注度,正是阿蒂亚所希望看到的。
在迈克尔·阿蒂亚爵士证明黎曼猜想的演讲中,约翰·冯·诺依曼的名字一再出现,英国老爷子说他的证明正是建立在冯·诺依曼的工作之上。
伽利略说:“自然界这部伟大的书是用数学语言写成的.”
著名物理学家詹姆斯·金斯爵士(SirJames Jeans,瑞利-金斯公式的提出者)说:“上帝是个纯粹数学家!”
无论是欧拉、黎曼还是冯·诺依曼、迈克尔·阿蒂亚,他们的一生其实只不过:做一个数学家、数学家、数学家。
03
我们可以在几乎所有数学的分支中见到欧拉: 从初等几何的欧拉线,多面体的欧拉定理,立体解析几何的欧拉变换公式,四次方程的欧拉解法到数论中的欧拉函数,微分方程的欧拉方程,级数论的欧拉常数,变分学的欧拉方程,复变函数的欧拉公式......
也就是说,从小学到博士,你在数学课上见过最多的名字是欧拉,你最经常写的符号如f(x)、sin、cos、tg,求和符号∑,自然底数e、圆周率π、虚数i这些符号都是他发明的。
不光是数学领域,欧拉喜欢把数学应用于自然科学,和冯诺依曼一样,他喜欢让数学与生活结合,喜欢跨界,从而为许多学科带来革命性的变革。
他用欧拉方程设计船舶—开启了流体动力学;
他用数学公式研究人体与声音--证明了耳膜与声波的共振,开拓了医学的领域;
他用数学来测量—发展了大地测量学;
他用方程计算人体血液流动--在生物学上添上重彩一笔;
他用欧拉数计算渠道断面--奠基了经典应用流体力学;
他用数学模拟老鹰的飞翔--建立了航空动力学、
他用数学计算年金保险 — 催生了投资的数学理论、
以他的欧拉函数为基础--计算机学上产生了广泛使用的RSA公钥密码算法;
他还曾涉足过这样几个学科:弹道学、分析力学、拓扑学、制图学,并最早尝试建立分子运动论。
欧拉作为算法大师,至今无人超越,这种机敏和犀利,如果一定要打个比方,就像最牛的打油诗人,像张打油,唐伯虎能霎时怼到你哑口无言、生无可恋。这种能力可谓 born to be,后天无法练就。

在柏林的 25 年中,他为普鲁士王国解决了诸如铸币、城市水道、运河、保险金和养老金制度等一系列重大的实际问题。他的卓越领导也使得濒临绝境的柏林科学院重获新生,逆袭成为欧洲影响力最大的科学院之一。
如有魔戒在手,欧拉所到之处总能硕果累累,生机勃发。
当时的宫廷里有许多能言善辩,口若悬河的哲学家,他们中最红的就是法国伟大的启蒙思想家伏尔泰,他常常喜欢把温厚的欧拉诱入哲学的迷宫,然后一帮朝臣们在旁边挤眉弄眼,在一片嘲笑声中,欧拉总是低头认输。
可是一旦遇上那些大牌哲学家鼓吹无神论,欧拉就不再淡定了,忘记了其实自己口才很一般,无畏地迎上前去。有趣的是,欧拉在辩论中常用的就是数学大招。
1766年英国著名哲学家和经济学家大卫.休谟来到普鲁士,休谟的无神论基本观点是:因为无人能从物质上或理性上证明上帝的存在,所以上帝根本不存在。休谟每到一处,都不忘宣讲他的无神论。
有次在爱丁堡,胖乎乎的休谟想横跨一片刚干枯的湖泊时,不小心滑入了泥沼中,胖子的悲哀就是一旦掉坑、必定被困、无法自救。这时一些卖鱼妇人刚好路过,但很快便认出他就是那位鼎鼎大名的无神论者,于是不肯救他,直到休谟答应要信教、并在泥沼中朗读主祷文和信经之后,这些壮硕的卖鱼妇才将他拉出泥坑。休谟得救后向朋友戏谑说这些卖鱼妇才是“他所遇过最聪明的神学家了”。
当时在宫廷迎战休谟的,竟然是一贯沉默寡言,低头认输的欧拉:“你知道什么是-1的平方根吗?它既看不见也摸不着,这个数字既不等于0,也不大于0,也不小于0 。按照你的逻辑,你该说:-1的平方根是不存在的物质,所以数学里不该有它。但是,如果没有负数的开平根,就不可能把12分解成两个数字之和,其乘积等于40。世界上看不见的,却深深存在于我们意识里的事物太多了,你知道吗?即使我们无法用物质去证明-1的平方根之存在,它事实上却存在着,否则数学都不存在了。因此,你所说‘无法用物质证明其存在的,其实就是不存在的’,这是大错特错!让我告诉你:上帝依然存在,即使无法用物质去证明。”
也许正是因为这场辩论,欧拉失去了工作。1766年,欧拉再次回到圣彼得堡,并在那里度过了生命中最后的十七年。
很多人说欧拉像一只鸟,终生挥着数学与信仰的双翼飞翔。
或许人们更应该惊叹于约翰·伯努利教授在欧拉还是青葱少年时的先见之明:『数学不会抖落他身上任何的敬虔信仰,而且你们看着吧,有一天他会成为数学界的神学家!』
所有人的老师-欧拉系列文章:




