读不懂明确而简单的例证？

戴榕菁

去年我证明了希尔伯特23个公开问题的第一个问题也就是所谓的康托连续性假说是错误的【[1]】之后，本以为当我给出了证明康托假说是错的简单明确的例证之后，一切都豁然开朗了，对于这个世界的读者来说不会再有什么解不了希尔伯特第一问题的纠结了；所以在那篇文章里我根本没把证明康托的结论是错误的作为重点来讨论，而是把从哲学上分析他为什么错了且一堆世界级的大咖们为什么会买他的账作为了重点-----这是因为我认为前半部分属于中学生的水平，而后半部分才是真正的高档次的论证。

遗憾的是，很快我就发现我错了：当今世界学术界的专业人员们还就似乎根本读不懂那属于中学水平的前半部分，就更别提一般的网络读者了。这里先简单回顾一下什么是康托的联系性假设以及我如何用简单的例证来证明它的错误：

所谓连续性假说（Continuum Hypothesis，缩写CH）是由著名集合论大师康托在1878年提出来，又被希尔伯特在1900年列为23个数学问题的第一个而且据说至今也没有明确答案的一个问题。其基本论点为：不存在这样一个集合，它的基数（即所含元素量）大于自然数集合的基数而小于实数集合的基数。

我的证明思路很简单：只要找到一个“基数大于自然数集合的基数而小于实数集合的基数”的集合就可以了。我给出的是下面这个集合：

其中m是自然数。很显然，(1)式的基数大于自然数而小于有理数。接着我又给出了一个无理数的集合：

其中n也为自然数，而且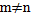。很显然，(2)式中的无理数是自然数的无穷多倍而它只是实数集合的一个子集。所以(1) 式的集合基数小于实数的集合。

至此，已经证明康托的联系性假说是错误的。

没想到当今学术界居然读不懂这么简单的证明逻辑，而他们拒绝承认我的证明的理由无不极其荒唐，其中比较典型的是：

1）连续性假说很多年前早被某人证明是正确的了。

2）希尔伯特的第一问题必须在他设定的条件下成立，那就是康托的集合论是正确的前提下成立。

上面的第1）个理由纯粹胡扯。我不是搞数学的，我之所以会卷入证明希尔伯特第一问题是错误的就是因为我被邀请参加academia.com的一个试图证明它是正确的讨论，而作为专业数学界人士的该讨论文章的作者在文章开头就说希尔伯特第一问题还没有被证明。我又去维基解密查了一下，那里说希尔伯特第一问题还没有公认地被证明或证伪，尽管有多人声称证明了。

上面的第2）个理由比纯粹胡扯的第1）个理由严重多了，已经属于纯粹放X了。

但是，尽管上面第2）个理由纯属放X，却很遗憾地是今天的丧失了基本哲学思考能力的专业学术界普遍能接受的理由。他们的逻辑是这样的：

你必须先承认对于无穷集我们必须用康托的一对一方法来衡量它的大小。如果你能找到一种可以将一个集合里元素和自然数一一对应机制，那么就认为那个集合的元素的数目和自然数一样多，也就是说那个集合的基数和自然数的基数一样大，或者说它是可数的；否则那个集合的基数就比自然数多，就是不可数的。根据这个定义，康托证明了实数的基数比自然数大，而有理数的基数和自然数一样大，接着就提出那个无法找出基数介于自然数和实数之间的集合的所谓的连续性假说。

这就相当于在篮球比赛中一方规定只有在三米以外的投篮才得分，而专长三米内进蓝的甲队输掉之后被别人笑话他们根本不会投篮一样。

为什么说专业学术界的上述逻辑纯属放X呢？理由很简单：

（一）根据前面给出的(1)式我们可以看出把有理数说成和自然数一样多是荒唐的，因此康托的上述度量无限集合的方法根本不能反映无限集合大小的本质。

如果作为一个俱乐部的人在节假日酒足饭饱之后沉迷于诸如猜谜语之类的消耗脑细胞的游戏的话，没人会在乎他们在折腾什么。可他们偏要由享誉世界的顶级数学家出面将那个连续性假说列为标志着人类数学最高水平的23个公开问题的第一个问题。这如果不是认知的错误的话，那就是故意戏弄世人。考虑到希尔伯特不可能是故意戏弄世人，所以这一定是认知上错误。这一定不是今天的学术界声称的必须在承认康托理论正确的前提下才成立的问题，而应该是希尔伯特错误地以为康托的理论是放之四海而皆准的正确理论，因此才将它作为他的23个公开问题的第一个问题提出的。也就是说在希尔伯特看来，这不是闭门俱乐部里的消耗脑细胞的游戏，而是一个严肃的有着普遍意义的数学基本问题。

换句话说，我们只有认为上面的第2）个理由是放X，才能还希尔伯特清白，才能表明希尔伯特只是认知上的错误，而不是故意玩弄世人！

（二）就算今天的专业学术界象对待具有狭义规则的游戏而不是放之四海而皆准的理论来看待康托的连续性假说，康托自己可不是那样看的。他根据他上述的度量无限集合的大小的法则得出著名的结论说：“一个正方形上的点数与正方形的一个边长的点数一样多。”这里他可没有声明他的结论只在他的特殊的游戏规则内才成立，而今天的世界各地大学的数学课堂里也仍然将康托的这个荒唐的结论作为放之四海而皆准的理论来讲述的，而不是作为狭义规则的游戏结果来介绍的。所以说，上面的第2）个理由根本就算是放X。它既不符合康托的原意也不符合希尔伯特的本意。

既然上面的第1）个理由是胡扯而第2）个理由是放X，那么它们就根本无法构成对于我的证明的否定。

此外，我上面给出的(1)式和(2)式可以是非常合理明确地对希尔伯特23个问题的第一个问题进行证伪的例证这一点也表明：对于无限集合，我们可以找出任意多的排列方式来，康托只不过在无限多种排列方式中找出了一种乍看上去很漂亮，但实际是在滥用（abuse）无限大概念的方式而已；他将之定义为度量无限集合的唯一法则，而淡漠了哲学思维的专业数学界就买了他的账。

你或许会问，今天的数学家们都这么白X吗？其实在康托出世不久前，丹麦的安徒生就已经对这个问题给出了答案：不是数学家们白X，而是他们将康托当成了皇帝，所以就把他的光腚看成了美丽的服装！

而我的文章则明确指出了康托集合的核心也就是康托用来度量无限集合的法则之虚幻和误导性，彻底否定了用康托一对一法则来度量无限集合的现实合理性。所以说，我文章所推翻的不仅仅是康托的连续性假说，而是康托集合的核心价值。

实际上，对康托集合论的核心价值的否定就自然推翻了康托的连续性假说也就是希尔伯特的23个公开问题的第一个问题。这就是为什么我在文章【1】中重点讨论的不是如何证伪康托的连续性假说，而是对康托集合论的哲学错误进行分析。

今天的主流学界和遍布世界的庞大科普队伍努力地给一届又一届的学子们营造这样的印象：学术发展的主要障碍是无法发现新的理论；所以要想取得学术突破就要努力发现新的理论，物理学和数学尤其如此。

但实际上，今天的学术发展的主要障碍是社会心理的障碍与社会政治的障碍，是对哲学的基本原则无知的障碍。今天专业学术界似乎已经完全忘了这样一个自古以来的哲学原则：真理高于权威！

唉，被错误哲学思维枷锁捆绑的学术界真的很可怜！更可怜的是现有的专业学术界永远不可能摆脱这样的枷锁！

 

 

 

---

[[1]] Dai, R. (2022). “Solution to Hilbert First Problem against the Illusion of Cantorian Cardinal System”. Retrieved from: https://wp.me/pkz9Y-8A