
空难发生在2025年1月29日下午8:48。一架载有60名乘客与4名机组人员的客机,对准了DCA的跑道,正在下降飞行;被一架有3名机组人员沿potomac河由北向南飞行的黑鹰直升机撞击,在空中爆炸形成一个火球;随后客机与直升机都沉入河中。下图右边是Kennedy中心的监控录像中在撞机前约八秒时的截图。在撞机前约八秒时,降落客机与起飞客机都正对Kennedy中心,由灯光亮点大小判断两[
阅读全文]
十七岁的中专生姜萍获得2024年阿里巴巴全球数学竞赛预选赛全球第十二名,被一些想当然地无端指责为造假,那些质疑的理由中唯一一个能成立的理由就是她的学历低,不如那些来自全球著名大学数学系的研究生本科生参赛选手。第一个问题,质疑者认为姜萍造假,那她到底抄谁的?她周围没有可供她抄袭的人。她周围没有著名大学数学系的高材生,只有一个不是著名大学的[
阅读全文]

只要用牛顿第二定律计算一下,就可以知道土星五(SaturnV)的那点推力是不能将载人登月舱送到月球的,只能把载人登月舱送到一个低高度绕地轨道(高度低于一千公里)上转几圈后再下来。打个非常简单的比方。三个宇航员乘神舟飞上了太空,多少天后他们乘坐返回舱软着陆于内蒙古的沙漠,安全回来了。他们到底去了哪里呢?当然他们是随天宫空间站在低高度绕地轨道上转了很[
阅读全文]
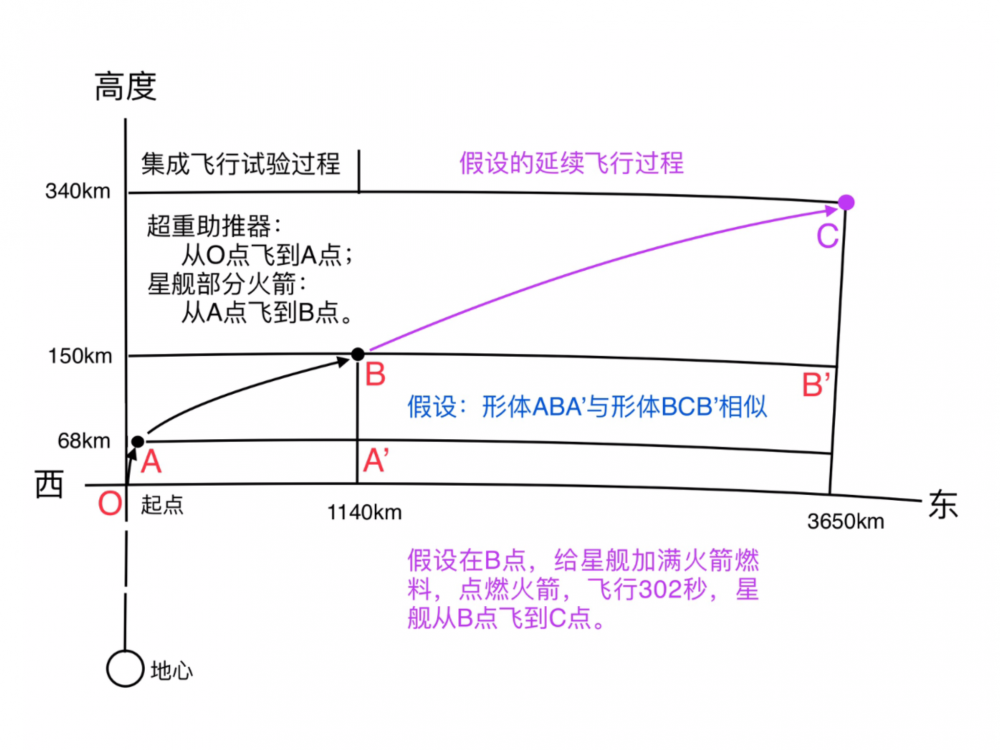
星舰第三次集成飞行试验成功地完成了:超重助推器的火箭燃烧了163秒,升到68公里的高度,速度达到1.597公里/秒;星舰部分的火箭燃烧了353秒,升到150公里的高度,速度达到7.357公里/秒。除了超重助推器留下了~310吨火箭燃料用于回收与星舰部分留下了~45吨火箭燃料用于重返大气层,全部能被用于星舰升高与加速的火箭燃料(3400-310=3090吨/助推器与1200-45=1155吨/星舰)都燃烧完了,[
阅读全文]
台海之战开打的具体时间,完全是美国定的。其实,台海之战与菲中南中国海之战都是美国对中国的西太平洋决战的前哨战。美国的战略目标就是要把台湾变成围堵中国的第一岛链的中心环节,夺取南中国海岛屿岛礁的主导权与归属分配权。如果美国不能取得在西太平洋对中国的军事优势,美国对中国的西太平洋决战就不可能开打,作为前哨战的台海之战与菲中南中国海之战[
阅读全文]
“赵安吉倒车落水过程”一文的逻辑是根据流体(空气,水)对物体运动(飞行,航行,包括游泳)的阻力,应用牛顿第二定律近似计算出一个最小速度,也就是,要求Tesla车飞落池塘的中央,在飞越堤坝时必须具备的最小速度。那么如果你在现场,应该如何救援赵安吉?尽管已是事后,简单地探讨一下也许会对今后有所帮助。当你目击或得知一起车祸,车飞入了池塘。既是本[
阅读全文]

从牧场内部的地图来看,要从客房B处到达主房A处,最近的路线是红色箭头旁的那条路,比较右下角google地图的长度标尺,估计其距离不超过250米,步行不超过三分钟。另一条路是黄色箭头旁的那条路,也就是从客房B处绕道C处再到达主房A处,估计其距离不超过450米,步行不超过五分钟。赵安吉描述的三点转弯掉头的地点就是客房南侧的停车场。
将上图客房部分放大。[
阅读全文]
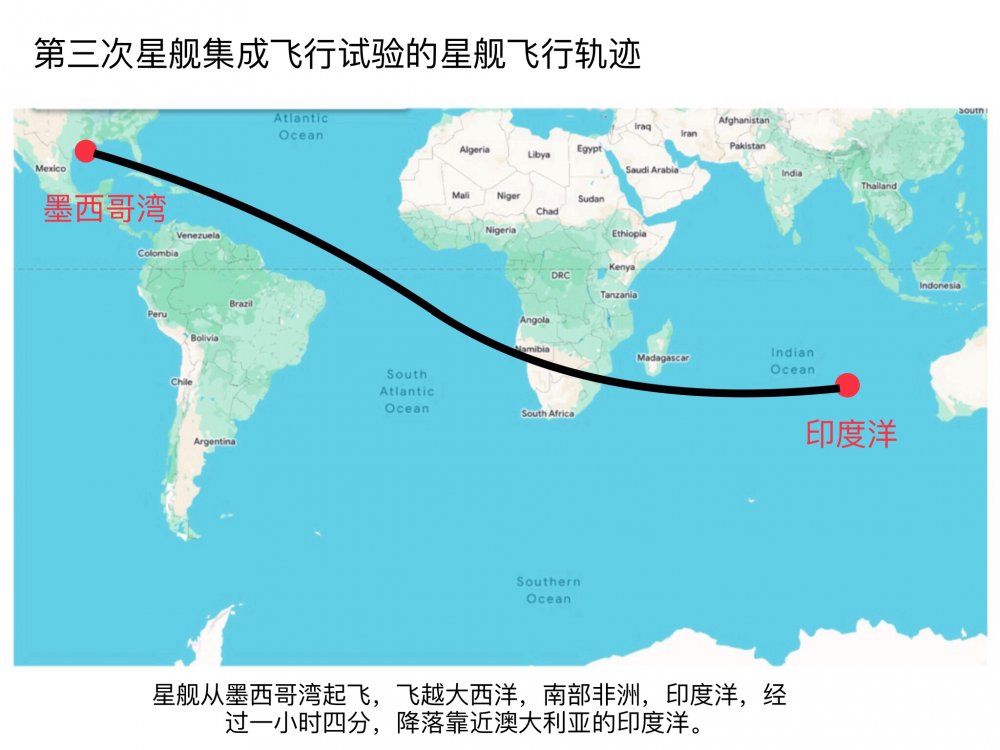
星舰第三次集成飞行试验于2024年3月14日进行,其结果:助推器火箭燃烧了163秒,升到68公里的高度,速度达到1.597公里/秒;星舰部分的火箭燃烧了353秒,最后升到150公里的高度,速度达到7.357公里/秒。这次试验成功完成了星舰火箭关闭及其之前的所有过程,也启动了在轨加注推进剂的演示,尝试了开启载荷舱门与关闭载荷舱门。对比2023年11月18日进行的第二次集成飞行试验的结[
阅读全文]
华尔街日报网发表文章认为:中国的人口政策是40多年前的误判,导致了中国提早出现老龄化,年轻女性数量逐年下降,年轻女性生育率降至更替率之下,生育低谷来临的速度比预期的快,从而引发了对超出想象的人口危机以及对中国人口结构崩溃的担忧,预计中国的人口到2100年下降到5.25亿。对于如何应对,中国束手无策。华尔街日报网描述的中国人口现状,恰恰说明中国在[
阅读全文]
亚铁氰化铁钾,即用于治疗铊中毒的普鲁士蓝,是一种颗粒很小的晶体,可以悬浮在水中。通过口服或灌胃进入肠胃,晶体表面的钾离子与肠胃里的铊离子相互交换形成亚铁氰化铁铊,可能是固体沉淀,然后经过粪便排除体外。根据英文维基百科:Itisgivenuntiltheamountofthalliumintheurinedropstobelow0.5mgperday.当每天经尿液排出的总铊量少于0.5毫克时,停止使用普鲁士蓝。一九九五年四月[
阅读全文]





