人类可能进行时间旅行吗？

时间旅行一直是许多的科幻小说，故事，电影的热门题材，也常被一些科学大师们所介绍。
每个人都会对时间旅行好奇：能回到过去又转回来多好啊！你可以回头重新做一生中的最重要的选择，也可反转你以前最后悔的事，当然也能轻易发大财--比如20年前买套北京的房子，买一万块钱的苹果或亚马逊的股票，今天绝对是千万身价了！
遗憾的是,时间旅行只能往前走，不能往回走--至少在宏观世界中是这样。时间不能往回走受的是是科学及现实的因果律所限定。一旦因果关系被破坏，一种现实上的孛论往往会出现。比如有人时间旅行到几十年前，在其母亲怀孕他之前把母亲亲手害死，结果造成他就不可能出生于世。既然他不存在，害死母亲的事件也不可能会发生，这样形成了一个因果关系互相矛盾，无法与现实相容了。
时间往前旅行则是可能的，比如宇航员到国际空间站生活，他们相对地球的人高速运动，所以他们的时间变慢了，几个月后他们回到地球，人会年轻了几个毫秒。当然，这点时间差别人体是无法感知的，年轻了几个毫秒也毫无现实的意义。
如果要体验到非常显著和令人向往的时间旅行，就必须有更高速的，甚至接近光速的飞船，目前人类的科技离这还太遥远。
本文打算进行一些理论上的探讨，至于科技和工程上的实现，一万年后大概希望也很小，就算留给一亿年后或更远将来的人类去伤脑筋吧--如果那时人类还没有毁灭的话。嘿嘿！
根据爱因斯坦的狭义相对论，当两个物体相对高速运动时，对方时间会变慢。假定从地球发射一个宇宙飞船，以接近光速飞向另一个星球--比如先说个小目标：一千光年距离的星球，（至于如几百万光年外的大目标，就留给科幻家们去考虑吧）飞船到达目的地后又以接近光速飞回。地球上的人都知道2000年后飞船会回来的--他们当然活不到那天，只能把记录留给几十代以后的子孙了。飞船上的人则幸运得多，假定他们飞船的速度达到光速的0.9999倍--比光速只慢万分之一，根据洛伦茨变换公式，他们的时间流逝会慢到为地球上时间的1/70.7，也就是地球上过了2000年，飞船上的人只过了28.2年，他们完全有机会看到2000年后地球的模样，也就是他们实现了超长的时间旅行！
到了这点，喜欢思考的人往往会提出一个严重的质疑：地球或飞船在相互运动中地位是平等的。地球上的人认为自己静止，飞船高速飞行，所以飞飞船上的时间变慢了。可反过来看，飞船上的人也可以认定自己的飞船没有动，是地球在高速地相对自己运动，所以地球上的时间应该变慢。双方的结论是完全相反的！到底谁的时间变慢了？还是都没有变？这就引出著名的双生子佯缪的问题！正式的结论是：一去一回的飞船时间变慢了。用上述的例子，飞船上的人度过28.3年回地球后，发现地球上已过了2000年！
要完整地解释这个疑问真的不容易，至今对绝大部分人来说仍是个百思不得其解的问题。
本文希望用一种图解的方式来详细分析其中的道理，这是楼主认为最明瞭的手段。
有愿意伤脑筋的人，欢迎继续往下读。如果你有高中以上学历，又希望真正懂爱因斯坦的狭义相对论，你的努力也许会对此知识有一个飞跃的提高啊。呵呵！
人们在看侦探悬疑小说时，总有一些读者受不了曲折惊险的情节所折磨而偷偷地先翻到书后去找到答案，嘿嘿！对于不想费脑太多的人，本文也在后边加了一个总结讨论部分，让你看到结果。当然如果对结论部分更为疑惑，那就再回头挑战自己吧！
在讨论之前，先说一下光速不变原理。光是个奇妙的东西，它在真空中的速度是29.9792458万公里/秒。不管发射者或接收者是处于静止或运动中，这个速度都保持不变。光速不变原理并非爱因斯坦发现，而是由美国物理学家Michelson–Morley在1887年发现，但爱因斯坦利用这个结果提出了狭义相对论。
时空图是描述宇宙空间运动的重要工具，为了简化讨论，这里空间只用了一维。
以下是用直角坐标画出的时空图：
 
图中ot为时间轴，os为空间轴。
oA代表一个运动物体的时间和空间的演变线，或称时空线。其中oT的长度代表A点的时间，oS的长度表示A点与运动出发点之间的距离。所以A的运动速度是oS/oT。我们把平行于os轴的TA线叫同时线（也称等时线），在同时线上不同距离的任何点，体系的时间都相同。把平行于ot轴的SA线叫等距线，在等距线上不同时间的任何点，体系到原点的距离相同。
时空图并不限于直角坐标，一个平行四边形的坐标也可表达为类似的时空图：
 
这里，ot'为时间轴，os'为空间轴。
类似于直角坐标，oA'为A’的时空线,其中oT'的长度代表A'点的时间，oS'的长度表示A'点到原点的距离。这里平行于os'轴的T'A'线是其同时线，而把平行于ot'轴的S'A'线是等距线。
当描述一束光在在直角坐标系统的运动时，oc为其时空线。这里，我们使用1年为一个时间刻度，1光年为一个空间刻度，双方刻度长度相同，TC/oT=1即代表了光的速度,因而，oC为两轴夹角的分角线，与两轴的交角都是45度。
 
类似，oc'表示光在平行四边形坐标系统的运动时空线，同样使用1年为一个时间刻度，1光年为一个空间刻度，双方刻度长度相同，T'C'/oT’=1即代表了光的速度，oc’为其坐标两轴的分角线，或它与两轴的交角相等。
以下的讨论使用一个直角坐标代表地球上的时空关系。假定从地球（原点）有一飞船出发飞行，oa为其运动的时空线，随着时间的流逝，它距原地越来越远。在此例子中，我们采用飞船速度为0.5倍的光速，用于较直观地讨论。
如果把飞船看为另一体系，该体系相对于地球体系运动，它的时空坐标可能是下图的平行四边形坐标，oa是其时间轴，os是其空间轴。
 
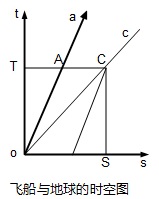
这坐标的时间与地球坐标是相同的，代表一种绝对的时间，或遵循所谓的牛顿的时空观。TA仍是它的同时线，或线上任何一点的时间都是oT的长度（时间刻度）。光的时空线对地球和飞船的时空系统都是相同的，oc即光的时空线。
对于这样的飞船时空坐标，一个问题将会显现出来：如果oA是1年（与oT相同），AC将会是0.5光年，明显小于TC的1光年。那样一来，飞船时空坐标的光速将是AC/oA=0.5。显然，光速不变原理在这样的飞船时空坐标中被破坏了！
为了让飞船时空坐标中光速保持不变，该时空图必须要修改。回到开始时描述的平行四边形坐标系统，oc’只有与两轴的夹角相等时，光速才可保持为1。为了达到两轴的夹角相等，从原点出发的空间轴os'将与原来的os轴分开，使飞船的时空坐标变成下图：
 
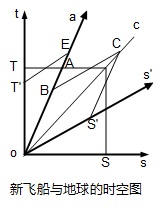
图中oS'/oB=1, 满足了光速不变原理。把os'与os分开是个非常重要的，革命性的变化！
在这新的飞船时空坐标中，既然它的os'轴与地球坐标的os轴已分开，它们对应的同时线也不再重合或平行。这种现象反映出了同时性的相对性，或不同体系的观察者对同时刻的观念将会分歧。
下面我们采用一个思想实验：假定地球或飞船上的人都有一种超距的观察能力，即各方可以瞬间（不受光传播速度限制）看到对方的时钟刻度，无论双方相距多远，并用“看”代表这种观察。
当地球人在1年的时刻T去“看”飞船上的时钟，根据洛伦茨变换公式，飞船上的时钟在A时刻的读数是0.866年（洛伦茨系数为0.866），这时地球人用的是TA的同时线。
当飞船上的人在自己的时钟为1年的时刻E点“看”地球的时钟，他使用的是飞船时空坐标中与os'平行的T'E同时线，该线与地球的时间轴交点T'的时间是0.866年！
以上的相互“看”对方的时钟，得出的结论都是对方的时钟变慢了，但是两个结果却并不矛盾，因为两边使用不同的同时线。这现象回答了“到底谁的时间变慢了”的争议。这点是个认知的飞跃！大家可以反复观看和领会同时线的意义，过了这一关，后面的讨论就容易理解得多。
在此也让大家注意到，飞船时空坐标的1年时间刻度比较长，其原因是时间变慢时，必须用更长的尺度代表1年。当飞船的速度越快和越接近光速，1年的刻度会越长。距离的刻度也有类似的性质。
既然在上述讨论中，双方都“看”到对方的时钟变慢了，为何最终飞船上的人能真正享受到因时间流逝较缓慢而比较年轻，而地球上的人却没有变化呢？
下一步将从旅行的细节来描述整个过程并解答以上的疑问。
 
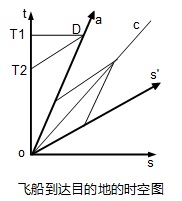
如果飞船多年飞行后（比如10年）接近了目的地D处，飞船将计划在D处停下并准备返回。
在到达10年的时刻，地球上的人去“看”飞船上的时钟，相似前文讨论，飞船上的时钟刻度为8.66年。
反过来在飞船一方，乘客已在飞船度过了8.66年，如果飞船仍然以0.5倍的光速前进而尚未开始减速，在乘客“看”地球的时钟时，他用的是与os'平行的T2D的同时线，与地球的时间轴交点T2的读数是7.5年(8.66年x0.866)。此时，双方都认为对方比自己年轻。
在飞船减速到停止的过程中，地球上的人“看”飞船的时间刻度仍是8.66年--因为减速时间较短，没有太大变化。
但是在飞船一方，它一旦减速停止下来，就与地球之间再也没有相对运动。此时，飞船的时空坐标会回归到与地球同一个直角坐标，或者双方都使用T1D的同时线。
戏剧般的变化发生在此刻：乘客“看”到的地球时间刻度不再是减速前“看”到的7.5年而是现在的10年。总之，在飞船减速的很短过程中，乘客“看”到的地球的时钟会从7.5年飞跃到10年，其原因是飞船的同时线由T2D到T1D的扫摆过程。
如果飞船的速度非常高而接近光速，这个跳跃会更大。比如飞船以光速的0.9999倍的速度（洛伦茨系数为0.0141）飞到1000光年外的目的地，当地球人过了1000年时去“看”飞船的时钟，读数为14.1年（1000年x0.0141)。飞船减速前，乘客如果此时去“看”地球的时钟，读数是0.2年（14.1年x0.0141），但一旦飞船减速后停下，再“看”到地球的时钟会从0.2年飞跃到1000年！
以上例子得出清楚的结论；高速飞船上的人，旅行后到达目的地度过的时间较少，与地球的人相比，比较年轻。
如果用双生子的例子可以有如下描述：双生子的哥哥乘坐飞船离开地球以0.5倍的光速行驶，地面上的弟弟10年后“看”飞船上的哥哥，发现哥哥只变老了8.66岁，比自己年轻了。哥哥在飞行8.66年后接近目的地，减速前“看”弟弟，发现弟弟只老了7.5岁，当然比自己年轻。可是飞船减速停靠在目的地后，哥哥再次“看”弟弟，发现弟弟突然增加了2.5岁，总共变老了10岁，比自己还老了。
当飞船从D处回程的旅行中，过程类似。
 
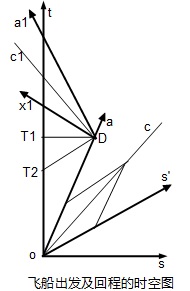
飞船加速前，双方共使用T1D的同时线，对应的地球时钟为10年，飞船的为8.66年。
返程光的运动时空线为Dc1，当飞船加速达到0.5的光速时，飞船的时空坐标将为平行四边形，它时间轴为Da1，空间轴兼同时线为Dx1。这时乘客再“看”地球的时钟，发现已从10年跳跃到了12.5年的刻度--同时线由T1D改变到Dx1的结果。飞船再次花了自己时钟的8.66年飞回地球，如果飞行途中继续“看”地球的时钟，可以发现地球的时钟在回程过程中只走了7.5年，比自己的时钟8.66年要慢，但因为出发加速时地球的时钟跳过了2.5年，所以地球的时钟在飞船回程中总共走了10年。整个算下来，飞船一去一回，地球上等了20年，而飞船上总共度过了8.66+8.66=17.32年。
等到飞船回到地球，大家当然可以面对面核对时钟，而无须在路途中必须依靠思想实验的超距“看”来观察对方时钟的进展，时间的差别这时成了眼见的事实。
总结讨论，算细账！
这里再把双生子佯缪的问题进行归纳，使用的飞船速度为0.5倍光速，其洛伦茨系数为0.866。在乘飞船的哥哥离开地球后，地球上的弟弟在20年后看到他回来。假定两方都有一种超距的观察能力，即各方可以瞬间（不受光传播速度限制）看到对方的时钟刻度，无论双方相距多远，并用“看”代表这种观察。
弟弟方：“看”到哥哥高速离去又高速回来，这家伙就只花了8.66年时间到了目的地，返回又用了8.66年。我这里没有什么动作，白白等了20年，所以现在他比我反而年轻了2.68岁，哼哼！
哥哥方：我的旅程分三部分，我一直在关心地球上弟弟的情况，所以有详尽记录。三部分的记载如下。
1. 我用了8.66年飞往目的地，一路上“看”到地球上的时钟比我的慢，弟弟似乎越来越比我年轻，因为我的8.66年，他才过了7.5年（8.66x0.866)。
2.我的飞船到了目的地以后还是以0.5倍的光速回飞，是否中间减速停下，或只是绕行转180度，一直以0.5倍光速继续飞，这些细节我就不讲了。总之，我开始回飞时（已是0.5倍的光速）专门“看”了地球的时间，发现地球的时钟从到达前的7.5年突然跳到了12.5年。我知道，我之所以“看”到的地球的时钟不同，是因为我的“同时”的观念发生了变化：前进时我的“同时”的观念与地球的时钟7.5年同时刻，返回时我的“同时”的观念与地球的时钟12.5年同时刻。所以，我这一转头，地球就度过了5年！
3.我用了8.66年从目的地飞回地球，一路上“看”到地球上的时钟比我的走得慢，我花了8.66年，地球那边时钟才走了7.5年。不过，加起来地球过了20年，我只用了17.32年！
综上所述，双生子的故事有了统一的结果：
弟弟看到哥哥因为高速行驶，时间变慢，他过了17.32年，自己等了20年，所以哥哥比我年轻2.68岁。
哥哥说，我飞去或飞回分别用了8.66年，飞行时弟弟的时间比我慢，他只度过7.5+7.5年，可是在第二阶段转向时，他的时间跳跃了5年，这是为什么弟弟实际过了20年，所以我比弟弟年轻2.68岁。
不少科普资料把双生子佯缪的解释留给广义相对论，也有的归于加速或减速时人类的生物反应造成飞船上的哥哥变年轻的原因。如果你搞懂了以上描述和讨论，你就知道那些都是因为谈不清楚而随便忽悠人的。嘿嘿！