地角天边
江郎才尽,不足为训
SAS编程技术教程(朱世武).zip_网盘链接页面 (sopandas.cn)
epdf.pub_applied-multivariate-statistical-analysis-6th-edit.pdf (archive.org)
统计学基本知识一 https://blog.csdn.net/fanzonghao/article/details/87929764
https://blog.csdn.net/qq_22592457/article/details/92982170
1、基础
因子:分类自变量;协变量:连续型自变量。
1.1 有关平均值参数u的假设检验
根据是否已知方差,分为两类检验:U检验和T检验。(当为μ即均值,σ是方差) 如果已知方差,则使用U检验,如果方差未知则采取T检验。【汪海波:当样本含量 n 较大时,样本均数符合正态分布,故可用 u 检验进行分析。当样本含量 n 小时,若观察值 x 符合正态分布,则用 t 检验(因此时样本均数符合 t 分布),当 x 为未知分布时,则应采用秩和检验。Wilcoxon的秩和检验(rank sum test)不依赖于总体分布的具体形式。】
1.2、有关参数方差σ2的假设检验
F检验是对两个正态分布的方差齐性检验,简单来说,就是检验两个分布的方差是否相等。【汪海波:t 检验和 u 检验不适用于多个样本均数的比较,因多次比较置信度下降。R.A.Fisher 的方差分析(analysis of variance,ANOVA)以 F 命名其统计量,又名 F 检验。】
1.3、检验两个或多个变量之间是否关联
卡方检验(Karl Pearson 卡方检验 - 知乎 )属于非参数检验,主要是比较两个及两个以上样本率(构成比)以及两个分类变量的关联性分析。根本思想在于比较理论频数和实际频数的吻合程度或者拟合优度问题。https://blog.csdn.net/qq_22592457/article/details/92982170
1.4 Wilcoxon的秩和检验
Wilcoxon_rank_sum test: SAS instruction (purdue.edu)
1.5 线性混合效应模型(linear mixed effects model)
1.5.1 https://blog.csdn.net/weixin_43569478/article/details/108079707
Linear Mixde Model, 简称LMM, 称之为线性混合模型。从名字也可以看出,这个模型和一般线性模型有着很深的渊源。线性混合模型是在一般线性模型的基础上扩展而来,在回归公式中同时包含了以下两种效应
fixed-effects, 固定效应
random efffects,随机效应
其名称中的混合一词正是来源于此。一元简单线性模型的公式如下:
其中X代表固定效应,ε表示随机误差,而线性混合模型的公式如下:
相比简单线性模型,多出了Z这一项,这一项称之为随机效应。当然两种模型的本质并不是体现在回归公式中自变量的多少,而在于自变量的类别,在一般线性模型中,其自变量全部为固定效应自变量,而线性混合模型中,除了固定效应自变量外,还包含了随机效应自变量。
所以关键之处在于判定自变量的类别,如果一个自变量的所有类别在抽样的数据集中全部包含,则将该变量作为固定效应,比如性别,只要抽样的数据中同时包含了两种性别,就可以将性别作为固定效应自变量;如果一个自变量在抽样的数据集中的结果只是从总体中随机抽样的结果,那么需要作为随机效应自变量。简而言之,如果抽样数据集中的自变量可以包含该自变量的所有情况,则作为固定效应,如果只能代表总体的一部分,则作为随机效应。
在分析的时候,可以将自变量都作为固定效应自变量,然后用一般线性模型来进行处理,那么为何要引入随机效应自变量呢?
使用一般线性模型时,是需要满足以下3点假设的:
正态性,因变量y符合正态分布
独立性,不同类别y的观察值之间相互独立,相关系数为零
方差齐性,不同类别y的方差相等
以性别这个分类变量为例,如果不同性别对应的因变量值有明显差异,也就说我们常说数据分层,那么就不满足上述条件了。此时如果坚持使用一般线性模型来拟合所有样本,其参数估计值不在具有最小方差线性无偏性,回归系数的标准误差会被低估,利用回归方程得到的估计值也会过高。
对于分层明显的数据,一种解决方案就是将不同的层分开处理,比如性别分层,那么就将不同性别的数据分开,每一类单独处理,但是这要求每一类包含的样本数据量要够多,而且分层因素的类别也不能太多,太多了处理起来也很麻烦。另外一个解决方案就是更换模型,使用线性混合模型。
一般线性模型有3个前提条件,而线性混合模型只保留了其中的第一点,即因变量要符合正态分布,对于独立性和方差齐性不做要求,所以适用范围更加广泛。
在线性混合模型中,随机效应变量Z的参数向量Γ服从均值为0,方差为G的正态分布,即Γ ~ N(0, G), 随机误差ε服从均值为,方差为R的正态分布,即ε ~ N(0, R), 同时假定G和R没有相关性,即Cov(G, R) = 0, 此时因变量Y的方差可以表示为
Var(Y) = ZGZ + R
在GCTA软件中,其核心就是线性混合模型,将所有SNP作为自变量,然后通过上述公式来估算SNP遗传力。
对于一般线性模型,可以通过最小二乘法或者最大似然法来估算其参数,对于线性混合模型,常用的参数估方法为约束性最大似然法
restricted maximum likelihood 简称REML, 对于如下的混合模型:
其中y是已知的,表示因变量的观测值,β是未知的,表示固定效应的参数向量,u是未知的,表示随机效应的参数向量,对于该方程的参数估计,其实就是求解β和u的值,公式如下
对于固定效应β, 其估计值为最佳线性无偏估计 best linear unbiased estimates(BLUE)
对于随机效应u, 其估计值为最佳线性无偏预测best linear unbiased predictors(BLUP)
线性混合模型只要求因变量服从正态分布,适用范围广,在遗传统计学中广泛使用。
1.5.2 线性混合效应模型入门之一(linear mixed effects model)
缩写LMM,在生物医学或社会学研究中经常会用到。它主要适用于内部存在层次结构或聚集的数据,大体上有两种情况:
(1)内部聚集数据:比如要研究A、B两种教学方法对学生考试成绩的影响,从4所学校选取1000名学生作为研究对象。由于学校之间的差异,来自其中某一所学校的学生成绩可能整体都好于另一所学校,换句话说就是学生成绩在学校这个维度上存在聚集现象。
(2)重复测量数据:比如要研究A、B两种降压药物对高血压患者血压的影响,在每个患者服药前、服药后1个月、3个月、6个月分别测量血压。由于同一个患者的每次血压之间存在明显的相关性,不能适用于传统的方差分析方法。
随机效应与固定效应
之所以称为“线性混合效应模型”,就是因为这种模型结合了固定效应和随机效应。
固定效应(fixed effect):所谓固定效应,指的是这个因素的每个水平(level)已经“穷举”出来了,不能或者不需要再做“推广”。比如上面的降压药物研究,虽然降压药物有很多,但是研究者只关心A、B两种药物的效果,所以可以视为固定效应。固定效应影响的是响应变量或因变量(如血压)的均值。
随机效应(random effect):指的是该因素是从一个更大的总体中抽取出来的样本,我们的研究结果要推广到整个总体。还是上面的药物研究,参与研究的患者只是一个小样本,所以患者作为随机效应。随机效应影响的是响应变量(血压)的变异程度即方差。

https://www.nature.com/articles/nmeth.3137.epdf
图a中演示是固定效应因子,每次重复实验,因子都是A1、A2、A3三个水平,三个水平的效应均值是固定的。
图b演示的是随机效应因子,每次重复实验,因子水平都不一样,如第一次是B1、B2、B3,第二次是B4、B5、B6,以此类推。所以因子的每个水平对均值的影响都是随机的,不固定的。
当然这两种效应有时并不是绝对的,主要还是看研究的目的。
线性混合效应模型入门之二 - 实例操作及结果解读(R、Python、SPSS实现
更新1:本文所用的数据下载地址: https://https://pan.baidu.com/s/1PYcMxDYgjjSvv9seUXmIDg?pwd=ngkw YgjjSvv9seUXmIDg?pwd=ngkw
更新2:评论区有人提出,R的结果和SPSS的结果不一致,这里解释一下,这是因为分类变量的类别参照不同,导致系数的符号相反,截距也不一样。R用的是0值(gender=0,micro=0,macro=0)作为参照,而SPSS用的是第一个出现的类别(gender=1,micro=1,macro=1)作为参照。两者结果数值不一样,但是本质是一样的。
--------------------------------------------------------------------------
下面以一个具体的案例,说明线性混合效应模型的操作及结果解读,本文以三种方式进行实现:分别是Python、R、SPSS。
案例数据介绍
本案例数据来源于一个肾脏病的研究。研究对200个肾病患者进行随访,每年化验一次肾小球滤过率(GFR,评价肾脏功能的指标,会逐年下降)。主要分析目的是探索基线的尿蛋白定量对GFR年下降率(斜率)的影响(尿蛋白量越大,对肾功能危害越大),混杂因素包括基线年龄和性别。
数据展示如下:
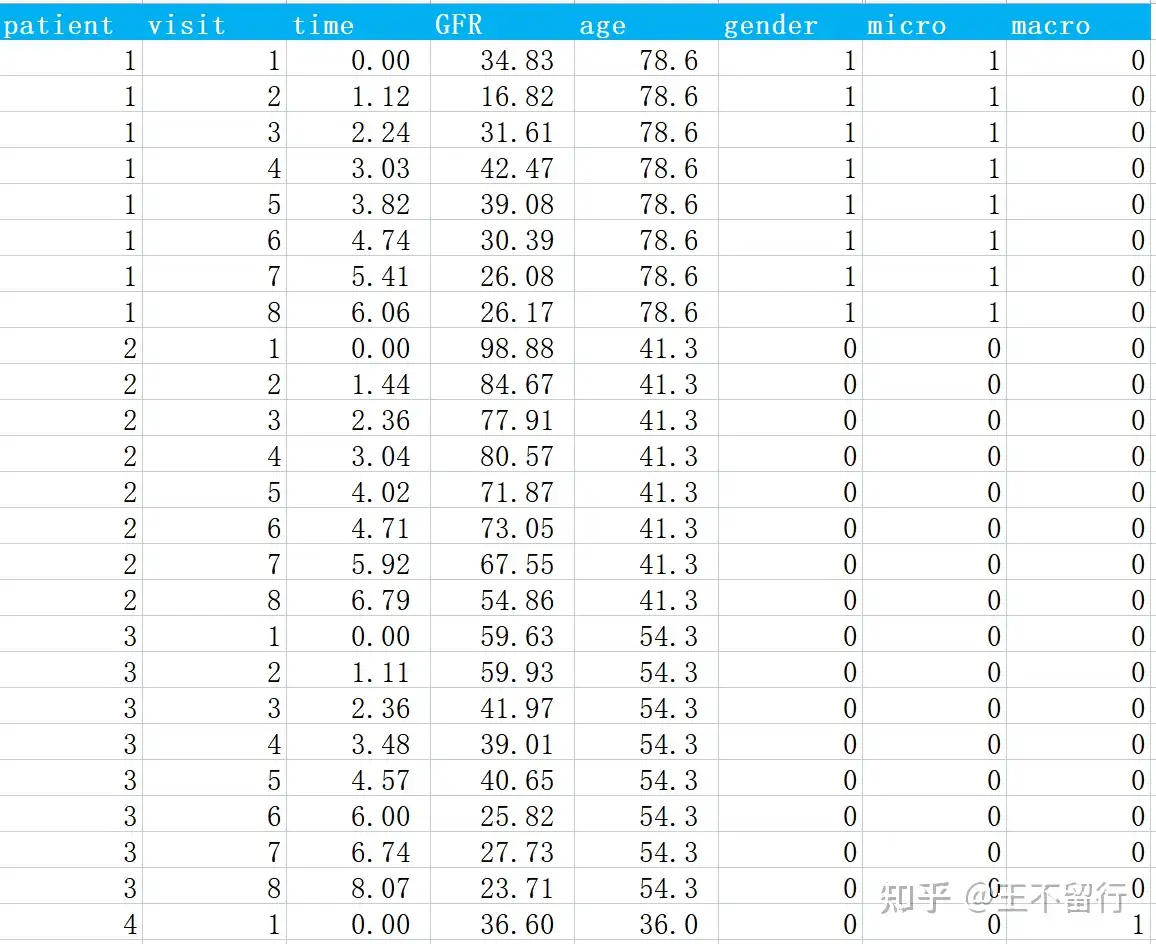
字段说明:
(1)patient: 患者ID编号;
(2)visit:化验次序编号;
(3)time:化验时间(单位年),第一次化验定为0,后面依次推延;
(4)GFR:肾小球滤过率,单位是ml/min/1.73^2,作为响应变量;
(5)age:基线年龄,单位岁;
(6)gender:性别,0=男,1=女;
(7)micro:基线是否有微量蛋白尿,0=无,1=有;
(8)macro:基线是否有大量蛋白尿,0=无,1=有;
补充说明:
(1)蛋白尿这里用了哑变量编码,macro=0且micro=0表示没有蛋白尿;
(2)数据中GFR化验数据有缺失,线性混合效应模型对缺失数据有良好的处理能力。
统计模型构建
由于一个患者进行了多次的GFR化验检查,属于重复测量数据,GFR不符合随机独立的要求。所以采用线性混合模型来建模。这里的响应变量是GFR,预测变量是基线年龄、性别、尿蛋白情况、化验时间、尿蛋白情况,其中尿蛋白是主要关注的因子。根据专业医学知识,我们假设尿蛋白不仅影响GFR的下降率,也影响基线GFR。所以预测变量还需要加上一个时间x尿蛋白的交互项(这里交互项的意思是说,不同的尿蛋白等级会有不同的GFR下降斜率和下降曲线)。另外假设性别、年龄仅影响基线的GFR,不影响GFR下降率(这个假设不一定合理,这里是为了模型简化,如果假设不成立,需要和尿蛋白一样乘以时间交互项)。用公式表示如下:
β1 等于基线时刻(time=0),在age和gender相同的情况下,微量蛋白组(micro)和正常蛋白组(micro=0且macro=0)人群基线GFR的均值的差值。
β2 等于基线时刻(time=0),在age和gender相同的情况下,大量蛋白组(macro)和正常蛋白组(micro=0且macro=0)人群基线GFR的均值的差值。
β3 等于正常尿蛋白组(micro=0且macro=0)人群GFR斜率的均值。
β4 等于微量蛋白组(micro)和正常蛋白组(micro=0且macro=0)GFR斜率均值的差值。
β5 等于大量蛋白组(macro)和正常蛋白组(micro=0且macro=0)GFR斜率均值的差值。
β3+β4 等于微量蛋白组(micro)人群GFR斜率的均值。
β3+β5 等于大量蛋白组(macro)人群GFR斜率的均值。
u0i 等于第i个患者和相同基线特征人群的基线GFR均值的随机偏差,服从均值为零和同方差的独立正态分布。
u1i 等于第i个患者和人群GFR斜率均值(如β3,β3+β4,β3+β5)的随机偏差,服从均值为零和同方差的独立正态分布。
eij 等于TIMEij时间的随机误差,服从均值为零和同方差的独立正态分布。
对照上文,我们就可以从统计软件得出的结果中找出对应的感兴趣的数据,进行相应的解释。
对照上文,我们就可以从统计软件得出的结果中找出对应的感兴趣的数据,进行相应的解释。
统计实现
1、R语言实现
核心代码:
library(nlme) # Fit Gaussian linear and nonlinear mixed-effects models
library(lme4) # Fit linear and generalized linear mixed-effects models
library(epiR) # Analysis of epidemiological data
library(epicalc) # Functions for epidemiological calculations
library(lattice) # Data visualization system
library(epiDisplay)
## IMPORT DATA
#-------------------------------
dropout.dat <- read.table("./data_dropout.csv", sep = ",", na.string = " ", header = TRUE, dec = ".")
## Linear mixed model
#-------------------------------
cat("LINEAR MIXED MODEL WITH SYMMETRIC COVARIANCE MATRIXn")
fit.m3 <- lme(GFR ~ time + age + gender + micro + macro + micro:time + macro:time,
random = list(patient = pdSymm( ~ 1 + time)), method = "ML",
data = dropout.dat, control = lmeControl(opt = "optim"))
# random argument: is identical to random = ~ 1 + time|patient
summary(fit.m3)
cat("95% CIn")
coef.fit.m3 <- summary(fit.m3)$tTable
ci(coef.fit.m3[,1], coef.fit.m3[,2], coef.fit.m3[,4])
cat("VARIANCE-COVARIANCE MATRIXn")
VarCorr(fit.m3)
输出结果:
> summary(fit.m3)
Linear mixed-effects model fit by maximum likelihood
Data: dropout.dat
AIC BIC logLik
9540.1 9602.84 -4758.05
Random effects:
Formula: ~1 + time | patient
Structure: General positive-definite
StdDev Corr
(Intercept) 10.426283 (Intr)
time 3.591427 -0.053
Residual 4.903330
Fixed effects: GFR ~ time + age + gender + micro + macro + micro:time + macro:time
Value Std.Error DF t-value p-value
(Intercept) 83.39609 3.242467 1175 25.719948 0.0000
time -1.74102 0.414817 1175 -4.197072 0.0000
age -0.28739 0.051564 195 -5.573483 0.0000
gender -2.61848 1.682065 195 -1.556703 0.1212
micro -18.39949 1.876851 195 -9.803381 0.0000
macro -26.56472 1.898283 195 -13.994078 0.0000
time:micro -2.92088 0.638801 1175 -4.572445 0.0000
time:macro -3.09101 0.670447 1175 -4.610374 0.0000
Correlation:
(Intr) time age gender micro macro time:micr
time -0.039
age -0.914 0.001
gender -0.018 0.000 -0.136
micro -0.169 0.067 -0.085 -0.002
macro -0.244 0.066 0.014 -0.108 0.425
time:micro 0.026 -0.649 -0.001 -0.002 -0.113 -0.043
time:macro 0.023 -0.619 0.001 -0.005 -0.041 -0.123 0.402
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.16590972 -0.60414300 -0.02061946 0.58097222 3.14244493
Number of Observations: 1378
Number of Groups: 200
> coef.fit.m3 <- summary(fit.m3)$tTable
> ci(coef.fit.m3[,1], coef.fit.m3[,2], coef.fit.m3[,4])
beta ci.low ci.up pvalue
(Intercept) 83.40 77.04 89.75 0.0000
time -1.74 -2.55 -0.93 0.0000
age -0.29 -0.39 -0.19 0.0000
gender -2.62 -5.92 0.68 0.1195
micro -18.40 -22.08 -14.72 0.0000
macro -26.56 -30.29 -22.84 0.0000
time:micro -2.92 -4.17 -1.67 0.0000
time:macro -3.09 -4.41 -1.78 0.0000
>
> cat("VARIANCE-COVARIANCE MATRIXn")
VARIANCE-COVARIANCE MATRIX
> VarCorr(fit.m3)
patient = pdSymm(1 + time)
Variance StdDev Corr
(Intercept) 108.70738 10.426283 (Intr)
time 12.89835 3.591427 -0.053
Residual 24.04265 4.903330
根据输出结果,我们整理成下表:
| 指标 | 估计值(95% CI) |
|---|---|
| 1、基线GFR差值(校正性别、年龄) | |
| (1)微量蛋白组(micro)-正常蛋白组差值 | -18.4(-22.1, -14.7) |
| (2)大量蛋白组(macro)-正常蛋白组差值 | -26.6(-30.3, -22.9) |
| 2、平均GFR年下降率(斜率) | |
| (1)正常蛋白组 | -1.74(-2.55, -0.93) |
| (2)微量蛋白组(micro)-正常蛋白组差值 | -2.92(-4.17, -1.67) |
| (3)大量蛋白组(macro)-正常蛋白组差值 | -3.09(-4.41, -1.78) |
2、SPSS 实现

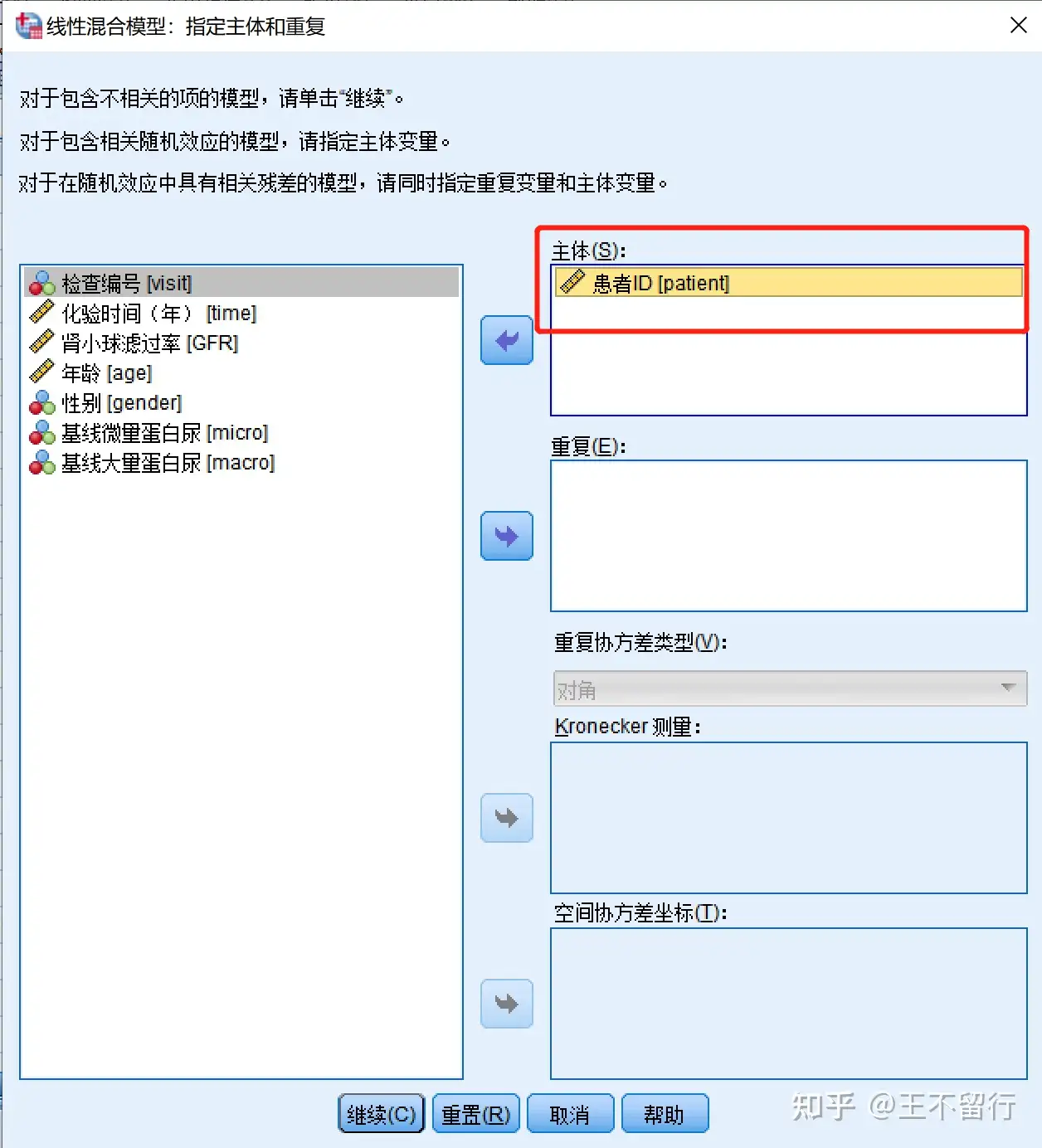
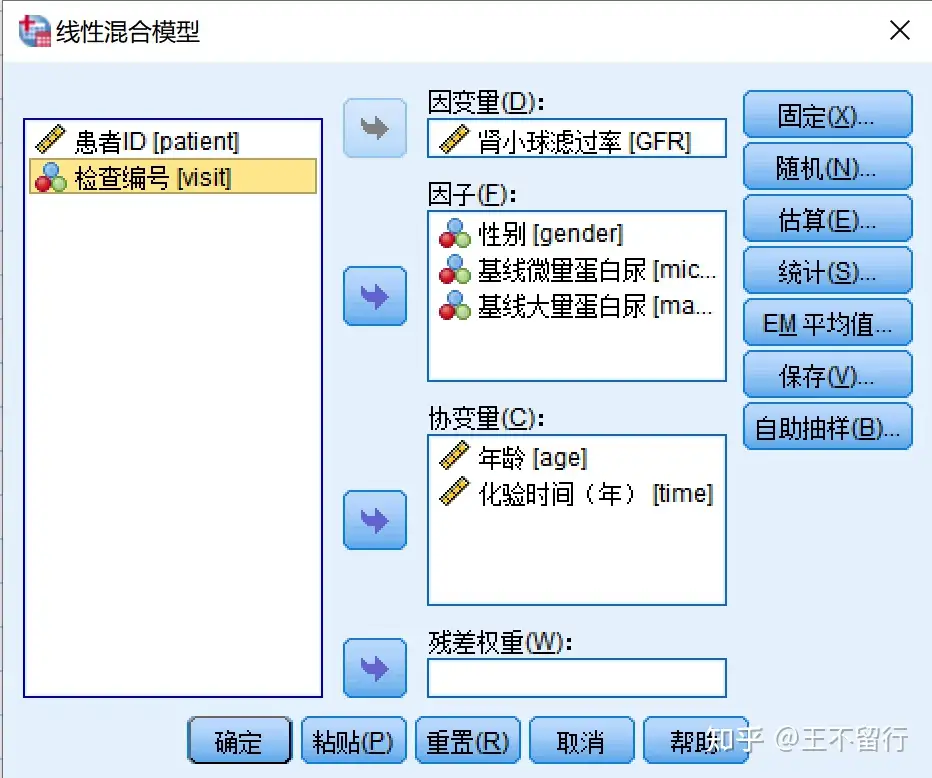
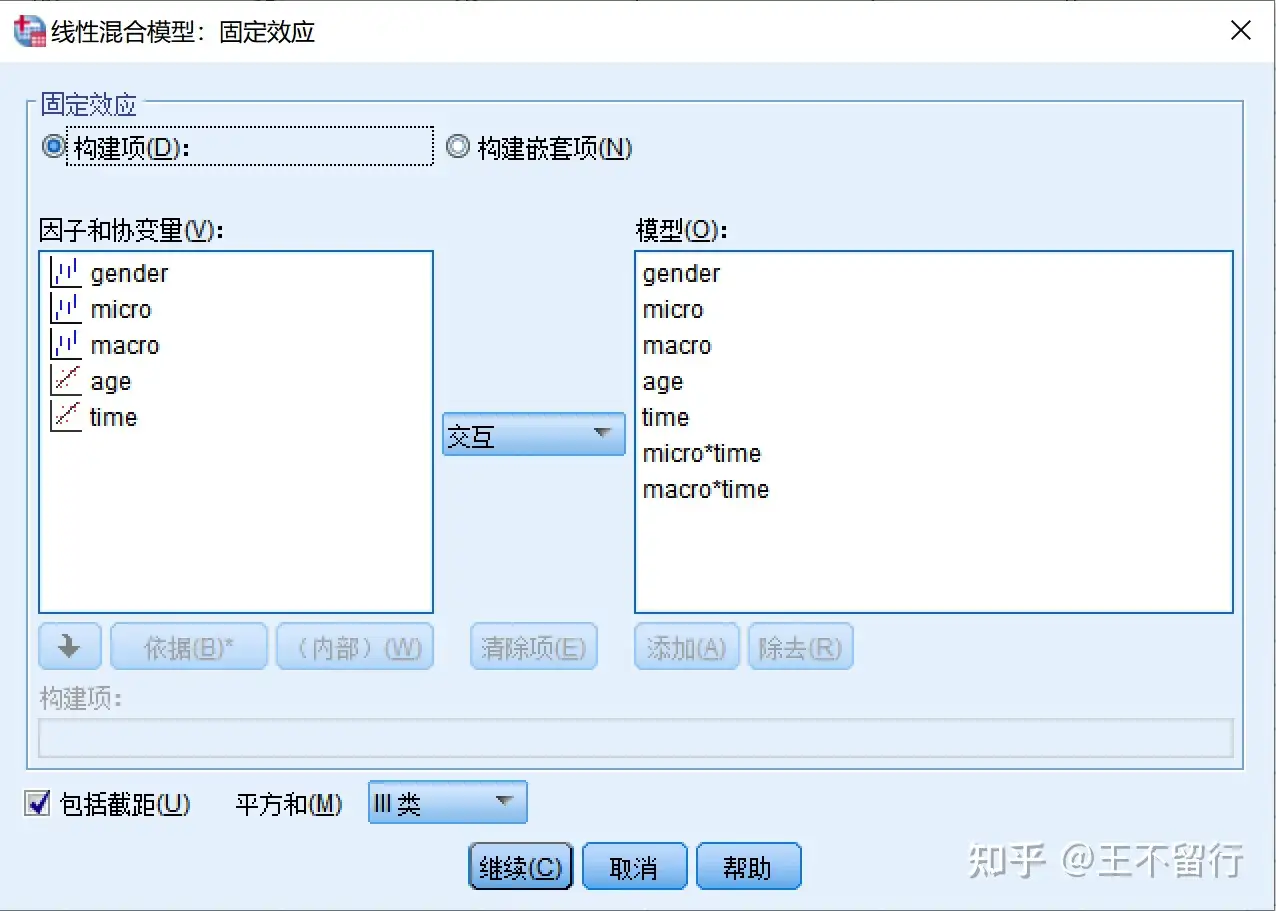
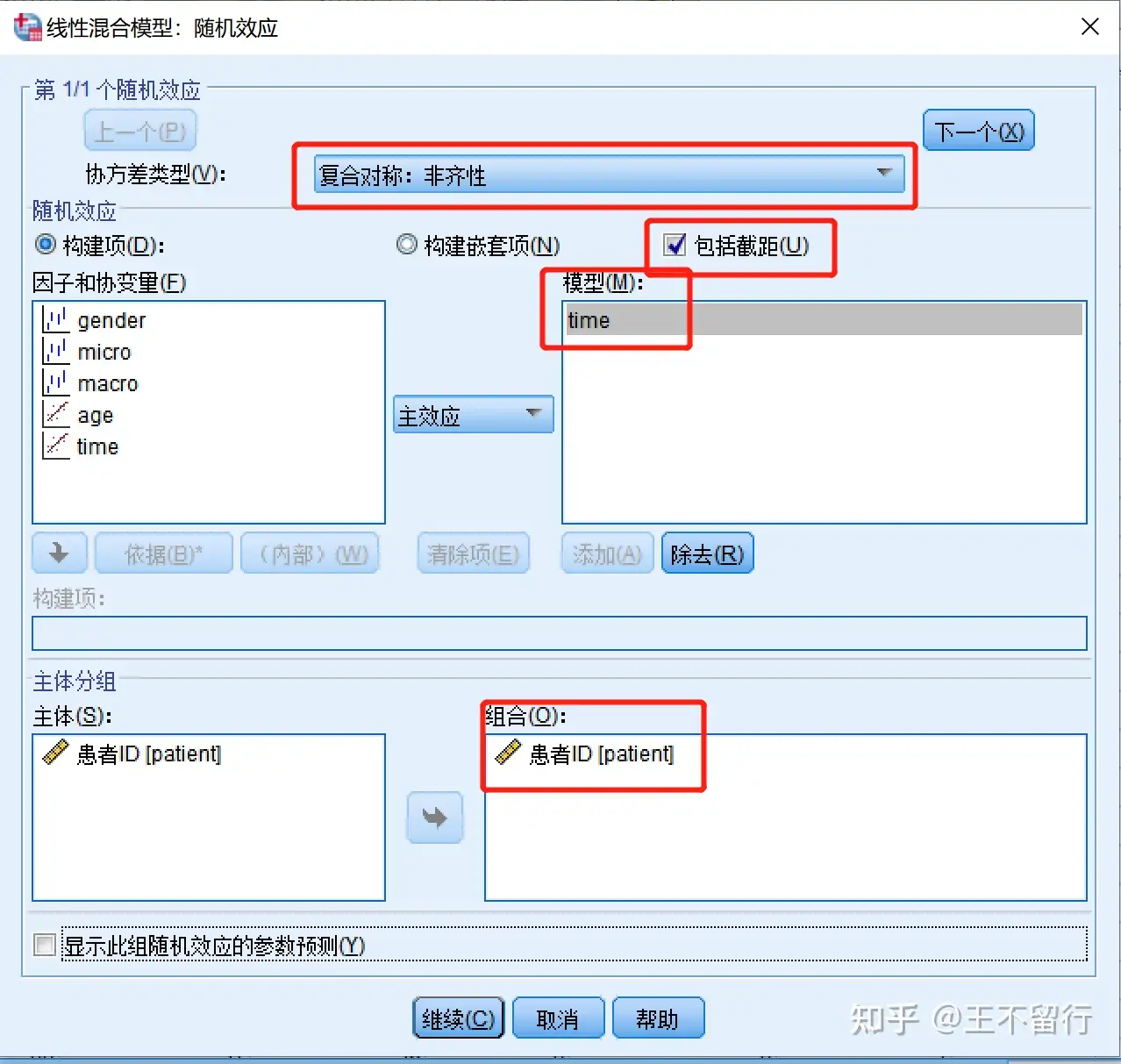

mango:此论文丢了一步即勾选统计量,点击Ok即可在左栏观察结果。SPSS9.2下得出的结果类似下述,估计值类似但标准差小些。
输出结果:
结果与R语言的一致。但是由于SPSS默认选择的分类变量参照不同,导致系数的符号相反,截距数值也不一样,本质是一样的。
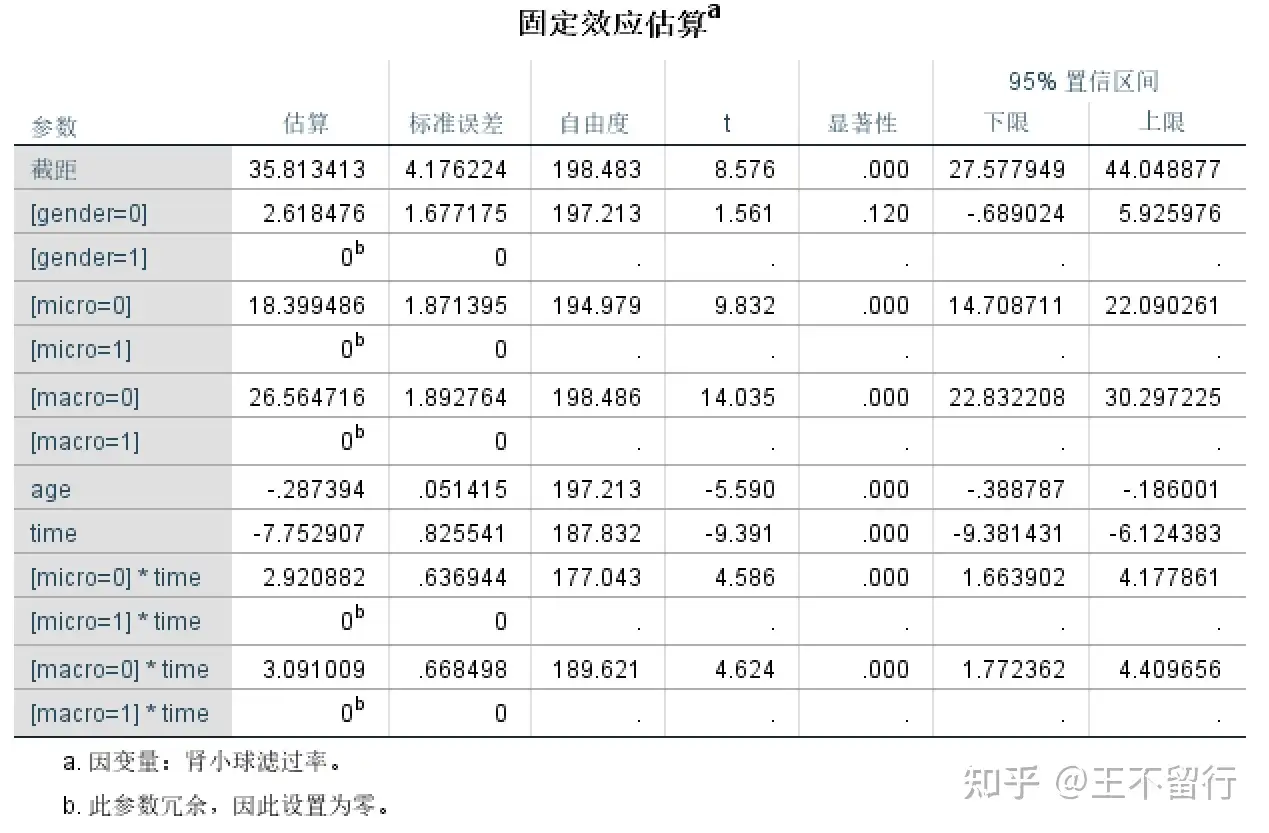
3、Python实现
Python的statsmodels包可以计算混合模型,但是计算开销比较大。可以在本地安装R环境,同时安装rpy2和pymer4,就可以用python调用R,非常方便。核心代码如下:
import pandas as pd
from pymer4.models import Lmer
data = pd.read_csv("./data_dropout.csv")
model = Lmer(formula="GFR ~ time + age + gender + micro + macro + micro:time + macro:time + (1 + time | patient)",
data=data)
model.fit()
print(model.summary())
输出结果:
Formula: GFR~time+age+gender+micro+macro+micro:time+macro:time+(1+time|patient)
Family: gaussian Inference: parametric
Number of observations: 1378 Groups: {'patient': 200.0}
Log-likelihood: -4754.489 AIC: 9508.979
Random effects:
Name Var Std
patient (Intercept) 111.803 10.574
patient time 13.130 3.624
Residual 24.038 4.903
IV1 IV2 Corr
patient (Intercept) time -0.054
Fixed effects:
Formula: GFR~time+age+gender+micro+macro+micro:time+macro:time+(1+time|patient)
Family: gaussian Inference: parametric
Number of observations: 1378 Groups: {'patient': 200.0}
Log-likelihood: -4754.489 AIC: 9508.979
Random effects:
Name Var Std
patient (Intercept) 111.803 10.574
patient time 13.130 3.624
Residual 24.038 4.903
IV1 IV2 Corr
patient (Intercept) time -0.054
Fixed effects:
Estimate 2.5_ci 97.5_ci SE DF T-stat P-val Sig
(Intercept) 83.402 76.984 89.820 3.275 192.390 25.469 0.000 ***
time -1.741 -2.559 -0.923 0.417 165.191 -4.174 0.000 ***
age -0.288 -0.390 -0.185 0.052 192.333 -5.521 0.000 ***
gender -2.616 -5.945 0.714 1.699 192.332 -1.540 0.125
micro -18.396 -22.111 -14.681 1.895 190.263 -9.705 0.000 ***
macro -26.565 -30.322 -22.808 1.917 193.610 -13.858 0.000 ***
time:micro -2.924 -4.182 -1.665 0.642 174.480 -4.552 0.000 ***
time:macro -3.096 -4.417 -1.775 0.674 186.786 -4.594 0.000 ***
2. SAS studio
由此:https://www.sas.com/profile/ui/#/sign-in 注册SAS账号,收到SAS账户激活邮件,激活账号并设置密码后,来到SAS Studio官网激活SAS OnDemand for Academics账户的用户ID,该用户ID会在后面用来登陆SAS Studio。登录:https://welcome.oda.sas.com u63668635
我们在程序标签页下运行「Proc setinint; run;」看看许可了哪些模块,结果发现除了常规的Base SAS、SAS/STAT、SAS/GRAPH、SAS EnterpriseGuid外,SAS/IML、SAS/ETS、 SAS/OR、 SAS/QC、SAS/CONNECT等模块也都赫然在列, 甚至连数据挖掘和文本挖掘的产品SAS Enterprise Miner 、SAS TextMiner以及可视化分析产品SAS Visual AnalyticsHub、Visual Analytics Explorer 、SAS Visual Analytics Services 都囊括在其中,不得说,SAS公司诚意满满啊。




