广义相对论，几乎全靠别人，为什爱因斯坦还如此伟大？

• 爱因斯坦闻名于世，都是因为狭义相对论和广义相对论。
• 狭义相对论，几乎呼之欲出，广义相对论，几乎全靠别人，为什爱因斯坦还如此伟大？

狭义相对论的建立：
爱因斯坦在建立狭义相对论时候，狭义相对论几乎是呼之欲出，洛伦兹和彭加莱等都做出了重要贡献。

• 广义相对论的建立：
• 数学储备不足，寻找数学工具靠：格罗斯曼。
• 建立方程数学不足，建立场方程靠：希尔伯特。
• 有了场方程，不会解场方程，解方程靠：弗里德曼和史瓦西。

这样叙述下来，感觉爱因斯坦什么都是靠别人，怎么就这么伟大？

原来，爱因斯坦仅靠一个核心思想，就名垂青史，照耀千古：

有一天，爱因斯坦坐在位于伯尔尼的办公室中，突然有了一个自己都为之“震惊”的想法。他回忆道：“如果一个人自由下落，他将不会感到自己的重量。”后来，他将此称为“我一生中最幸福的思想”。

这个自由落体者的故事已然成为了一个标志，与其他关于引力发现的绝妙故事(伽利略在比萨斜塔投掷物体以及牛顿被苹果砸中脑袋)一样，这些事迹都只是经过美化、杜撰的民间传闻罢了。爱因斯坦更愿意关注宏大的科学议题，而非“琐碎的生活”，他不太可能因看到一个活生生的人从屋顶跌落而联想到引力理论，更不可能将此称为一生中最幸福的思想。

不久，爱因斯坦进一步完善了这个思想实验，他想象自由落体者处在一个密闭空间中，比如一部自由坠落的升降机。在这个密闭空间中，自由落体者会感到失重，并且他抛出的任何物体都会与他一起漂浮。他将无法通过实验来辨别，自己所处的密闭空间是正在以某一加速度做自由落体运动，还是正在外太空的无重力区域漂浮。

然后，爱因斯坦想象这个人仍在同一个密闭空间里，处于几乎没有重力的外太空中。此时有一个恒力将密闭空间以某一加速度向上拉升，他将会感到自己的脚被压到地板上。如果此时，他抛出一个物体，那么该物体也将会以加速运动落在地板上，就如同他站在地球上一样。他没有任何方法能够区分，自己是受到引力的作用，还是受到向上加速度的作用。爱因斯坦称之为“等效原理”(the equivalence principle)。以局域效应来看，引力和加速度是等效的。因此，二者是同一种现象的不同表现形式，即可以同时对加速度和引力作出解释的某种“宇宙场”(cosmic field)。

接下来，爱因斯坦花费了8年时间，把这个自由落体者思想实验，改写成为物理学史上最优美、最惊艳的理论。

 

如果非要较真，实际上是亨德里克·安东·洛伦兹最早推导出来了洛伦兹因子.

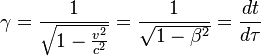
他离狭义相对论只有一步之遥，但他始终没有去推翻牛顿的经典力学体系。庞加莱是属于用数学的思维构建了相对论原型出来，洛伦兹是在研究电子运动的试验中的得出了洛伦兹因子的。爱因斯坦曾表示洛伦兹对他的研究发现起到了很重要的启发作用。所以说，狭义相对论的诞生，并不只有爱因斯坦一个人在努力，但是仅凭狭义相对论，爱因斯坦是无法得到这么高的评价的。

亨利·庞加莱比爱因斯坦还早开始向这个方向思考，但是庞加莱推导出质能公式实际上比爱因斯坦晚了几个礼拜,和爱因斯坦写出的几乎一模一样，但与爱因斯坦不同的是他用的是纯数学的思想来构建，并没有思考太多实际的物理意义，因此当庞加莱一看到爱因斯坦的论文就大有英雄所见略同的感觉，但庞加莱非常谦虚，他一面义务帮爱因斯坦宣传他的理论，一面不断的告诉人们是爱因斯坦第一个发现了相对论。

丘成桐：
广义相对论的这个方程，通过一百年的观察，基本上都是正确的。爱因斯坦跟希尔伯特互相竞争，也互相帮忙。1915年，二人相遇。他们之间的讨论激发了两人的灵感并促成了广义相对论中爱因斯坦运动方程的诞生（希尔伯特发现了希尔伯特作用量，可以用来简洁地推导爱因斯坦方程，而爱因斯坦直接创建了这个方程）。数学家希尔伯特甚至比爱因斯坦更早地推导出了这个方程。

爱因斯坦发觉他的方程可以用来解释时空和物质的分布是互相影响的，不像牛顿力学里面认为的时空是固定的，时间和空间是没有关系的。他发觉时空不停在改变。发现这些方程可以用来解释光线偏折。在此过程中，爱因斯坦做出了一个基础性的概念突破：不仅仅物质的存在产生重力从而弯曲时空纤维，而且重力直接来源于时空的曲率。过了不到两年，天文观察证实了这个发现。1918年，爱因斯坦因此一举成名。这是一个划时代的观念上的大突破。

爱因斯坦方程有很多不同的解，因为爱因斯坦在构造这个方程的时候，他找到了方程，可是并没有限定这个解的唯一性。这个解有它的边界条件，有它的初始条件，这两个条件爱因斯坦都没有解决。不但不晓得，直到现在过了一百年以后，我们对这个问题还是在辩论。爱因斯坦在1915年发现这个方程，不到一年，当时正研究球形对称星系如何影响重力的史瓦西（Karl Schwarzschild）发现爱因斯坦方程的一组解，这个解是球对称的（史瓦西解可以应用于单一球状行星的天文研究）。

 

史瓦西解让爱因斯坦得以计算并观察很多引力场的重力是怎么样的。通过这个解，我们可以模拟太阳系：行星的质量远轻于太阳，它们在史瓦西几何里可以被看成是沿着测地线移动的微粒。测地线可以通过计算得到，它们不必是闭合的圆周。例如水星的运行轨道已经被发现是一个具有微小偏差的圆形轨迹，每世纪进动43秒。同时，史瓦西解还有助于推算光线弯曲度。正如爱因斯坦所预测的，太阳产生的重力会改变时空的几何。因此，从行星射向地球的光线在经过太阳附近时会产生弯曲。通过计算史瓦西几何中的零测地线，可以推算光线的弯曲度。计算结果与实验数据的吻合令人满意。这是这一重力的新理论开创初期所取得的重要成就之一。

 

史瓦西解在今天依然重要，我们做全球定位GPS的时候，仍然要用到这个解。因为地球是一个重力场，我们的光线受到这个重力场的影响，假如不用这个解的话，算出来的结果不对。史瓦西解让我们知道光线通过太阳的引力场时会有偏差，这是很重要的成就。

广义相对论受到黎曼几何发展的重要影响，反过来讲，爱因斯坦所取得的巨大成功深刻影响了黎曼几何的发展。在广义相对论提出之后，几何学家认识到了爱因斯坦度量的美——特别是那些满足真空爱因斯坦方程的度量。