子夜读书心筆

写日记的另一层妙用，就是一天辛苦下来，夜深人静，借境调心，景与心会。有了这种时时静悟的简静心态，才有了对生活的敬重。

首页文章列表博文目录

个人资料

不忘中囯 (热门博主)

给我悄悄话

博客访问：

财经观察 1566 --- Taylor rule

(2008-11-28 00:16:39) 下一个

From Wikipedia, the free encyclopedia

Jump to: navigation, search

A Taylor rule is a monetary-policy rule that stipulates how much the central bank should change the nominal interest rate in response to divergences of actual GDP from potential GDP and of actual inflation rates from a target inflation rates. It was first proposed by the by U.S. economist John B. Taylor in 1993.^[1] The rule can be written as follows:

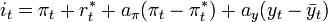
$i_t = \pi_t + r_t^* + a_\pi ( \pi_t - \pi_t^* ) + a_y ( y_t - \bar y_t )$

In this equation, $i t$ is the target short-term nominal interest rate (e.g. the federal funds rate in the US), $π t$ is the rate of inflation as measured by the GDP deflator, 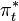$\pi^*_t$ is the desired rate of inflation, 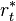$r_t^*$ is the assumed equilibrium real interest rate, $y t$ is the logarithm of real GDP, and 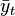$\bar y_t$ is the logarithm of potential output, as determined by a linear trend. A possible advantage of such a rule is in avoiding the inefficiencies of time inconsistency from the exercise of discretionary policy.^[2]^[3]

Interpretation

According to the rule, both $a π$ and $a y$ should be positive (as a rough rule of thumb, Taylor's 1993 paper proposed setting $a π = a y = 0.5$ ). That is, the rule "recommends" a relatively high interest rate (a "tight" monetary policy) when inflation is above its target or when the economy is above its full employment level, and a relatively low interest rate ("easy" monetary policy) in the opposite situations.

Sometimes monetary policy goals may conflict, as in the case of stagflation, when inflation is above its target while the economy is below full employment. In such a situation, the rule offers guidance on how to balance these competing considerations in setting an appropriate level for the interest rate. In particular, by specifying $a π > 0$ , the Taylor rule says that the central bank should raise the nominal interest rate by more than one percentage point for each percentage point increase in inflation. In other words, since the real interest rate is (approximately) the nominal interest rate minus inflation, stipulating $a π > 0$ is equivalent to saying that when inflation rises, the real interest rate should be increased.

Although the Fed does not explicitly follow the rule, many analyses show that the rule does a fairly accurate job of describing how US monetary policy actually has been conducted during the past decade under Alan Greenspan.^[4]^[5] Similar observations have been made about central banks in other developed economies, both in countries like Canada and New Zealand that have officially adopted inflation targeting rules, and in others like Germany where the central bank's policy did not officially target the inflation rate.^[6]^[7] This observation has been cited by many economists as a reason why inflation has remained under control and the economy has been relatively stable in most developed countries since the 1980s.

During an Econtalk podcast Taylor explained the rule in simple terms using three variables: inflation rate, GDP growth, and the interest rate. If inflation were to rise by 1%, the proper response would be to raise the interest rate by 1.5% (Taylor explains that it doesn't always need to be exactly 1.5%, but being larger than 1% is essential). If GDP falls by 1% relative to its growth path, than the proper response is to cut the interest rate by .5%.^[8]

Critique

Orphanides (2003) claims that the Taylor rule can misguide policy makers since they face real time data. He shows that the Taylor rule matches the US funds rate less perfectly when accounting for these informational limitations and that an activist policy following the Taylor rule would have resulted in an inferior macroeconomic performance during the Great Inflation of the seventies.^[9]

References

^ Taylor, John B. (1993): Discretion versus Policy Rules in Practice, Carnegie-Rochester Conference Series on Public Policy 39, 195-214.
^ Athanasios Orphanides (2008). "Taylor rules," The New Palgrave Dictionary of Economics, 2nd Edition. v. 8, pp. 200-04.Abstract.
^ Paul Klein (2009). "time consistency of monetary and fiscal policy," The New Palgrave Dictionary of Economics. 2nd Edition. Abstract.
^ Clarida, Richard; Mark Gertler; and Jordi Galí (2000), 'Monetary policy rules and macroeconomic stability: theory and some evidence.' Quarterly Journal of Economics 115. pp. 147-180.
^ Lowenstein, Roger (2008-01-20), "The Education of Ben Bernanke", The New York Times, http://www.nytimes.com/2008/01/20/magazine/20Ben-Bernanke-t.html
^ Bernanke, Ben, and Ilian Mihov (1997), 'What does the Bundesbank target?' European Economic Review 41 (6), pp. 1025-53.
^ Clarida, Richard; Mark Gertler; and Jordi Galí (1998), 'Monetary policy rules in practice: some international evidence.' European Economic Review 42 (6), pp. 1033-67.
^ Econtalk podcast, Aug. 18, 2008, interview conducted by Russell Roberts, sponsored by the Library of Economics and Liberty.
^ Orphanides, A. (2003): The quest for prosperity without inflation, Journal of Monetary Economics 50, p. 633-663.

External links

[ 打印 ]

[ 加入书签 ]

阅读 () ┆ 评论 (0)

目前还没有任何评论

登录后才可评论.