科学家研究自然不是因为它有用;他研究它,因为他喜欢它,他喜欢它,因为它很美。如果自然不美,就不值得了解,如果自然不值得了解,生活就没有价值。当然,我在这里不是说那种触动感官的美,品质和外表的美;并不是说我低估了这种美,远非如此,而是它与科学无关;我的意思是来自各部分的和谐秩序的更深刻的美,纯粹的智慧可以理解”。 - 亨利庞加莱
“在我长达 45 年的整个科学生涯中,最令人震惊的经历是认识到爱因斯坦广义相对论方程的精确解,由新西兰数学家罗伊克尔发现,提供了无数未知数的绝对精确表示。填充宇宙的大质量黑洞的数量。这种在美面前颤抖”,这一令人难以置信的事实,即在数学中追求美的发现应该在自然中找到它的精确复制品,这一事实说服我说美是人类心灵最深刻和最深刻的反应.”——苏布拉马尼扬·钱德拉塞卡
数学现实表示数学对象的世界、它们之间的关系、结构、逻辑结论、方法论以及理论物理学的辉煌大厦简洁地捕捉到的一切。它与理论物理学有细微的不同,因为它对理论物理学的数学方面具有更大的意义,尽管不像严格的数学物理学那样过多地涉及纯数学方法。
对自然法则的探索也许是所有探索中最令人着迷的,它象征着西方有史以来最伟大的问题:“它是什么?” 补充了有史以来伟大的东方问题,“我是谁?”。“这是什么?” 指客观现实。现在,客观现实的出现被大脑感知为某种模式,并作为一种感知呈现给大脑,而大脑又将其作为一个概念呈现给智能。在这种从大脑到心智和智能的过渡过程中,知觉本身变形为一种远离原始经验的符号,也就是说,远离普通语言。由此产生了一个象征性对象、形式和关系的世界,赋予感知世界以意义。正是这种将意义注入感知的原始世界,才是欣赏数学的真正关键。自从柏拉图提出他的“edios”作为先于客观世界以来,数学家和自然哲学家之间就这些世界的优先性一直存在争论。尽管如此,不可否认的是,应用于物理学的数学造就了理论物理学这个极其美丽的领域,它代表了人类最深刻和最高的创造力。
BS Ramachandra 博士自己的生活和工作是梦想的组成部分,因为它代表了他对理论物理的痴迷和他的深刻目的,即用他通过致力于研究而获得的敏锐洞察力重新点燃和振兴聪明的年轻人的教育。生活完全以学习、研究和奖学金为中心。一个8、9、10年级连续不及格,差点迷失在学术界的天才学生,11、12年级又跳回了学业阶梯的顶端,之后加入了工程学院从事机械工程,对理论物理产生兴趣并全神贯注于它几乎排斥其他一切,BS Ramachandra 的生活和工作确实是造就梦想的东西......没有其他科学家和教育家可以声称像 BS Ramachandra 博士一样利用数百名聪明的年轻人进入非凡的学习和研究水平。CFRCE 的革命仍在进行中,并且如火如荼。
下面是 Karthik Bharadwaj 与 BS Ramachandra 博士关于他的网站“数学现实”的意义和目的的对话。
KB:我认为最好从“数学现实”这个名字开始。你说这是什么原因?
BSR 博士:我正在寻找一个合适的名字来表达我将要写理论物理中的真与美的事实。在我攻读理论物理学博士学位的早些年里,我更多地受到数学美感的激励,而不是某个特定理论包含或产生的真理。并不是说我不关心“真相”。事实上,这是我选择理论物理而不是纯数学的主要原因。我说纯数学是很严肃的,因为在我开始攻读博士学位的两年前,我已经专门研究纯数学近四年了,几乎不包括理论物理。
我读了几卷 J Dieudonne 的“分析论”和 Serge Lang 的许多书,当然还有亚伯拉罕和马斯登的“力学基础”,仅举几例。但在沉浸在纯数学中的那段短暂时间之后,我被一种深刻的数学美感强行带回了理论物理学。所以一年前,当我想到写我的见解和观点时,我想到将真与美与宁静和洞察力融合在一起,“数学现实”这个词自然而然地出现在我的脑海中。
KB:既然你提到了它,你能谈谈你是如何进入理论物理学的吗?我认为这将为您经常谈论的“任务”一词提供一个非常需要的视角。
BSR 博士:当然。我遇到了“理论物理学”这个词,显然是偶然的,但实际上是由于我的深入探索而半意识地偶然发现的。许多人可能不知道,直到我 7 年级,我还是一个传统上聪明的学生,在班上名列前茅。但是在我 8 年级和 9 年级的时候,我的学业出现了令人震惊的下降,我的学业成绩一落千丈,实际上我在班上获得了第 33 名,被称为全校最差的学生!然而,在我 10 年级的时候,我意识到我已经陷入了危险,我正在坠入深渊,无法再爬回去。我付出了巨大的努力,并跳回了学术阶梯的更高梯级。
所以在我 12 年级之后,我发现自己加入了一所工程学院,攻读机械工程学士学位课程。现在距离工程学院开学还有大约五个月的时间。我在 11 年级和 12 年级对物理和数学产生了兴趣,所以我继续独立学习数学和物理。我去书店买了一些数学和物理方面的高级书籍。我想正是在这个时期,“理论物理学”这个词让我印象深刻。我认为是在费曼物理学讲座中。但最初我并没有那么重视它,尽管它无疑引起了我的兴趣。
五个月的时间结束后,我怀着深深的追求,急切地去了工学院,更想进图书馆而不是上课。您必须记住,在互联网出现之前的那个时代,图书馆是书籍的唯一来源,尤其是关于高等数学和物理学的书籍。于是我去大学图书馆看了看。有两本书引起了我的注意。其中一个是 Morse 和 Feshbach 的一本漂亮的银色书,“理论物理方法”。另一个是 Bjorken 和 Drell 的“相对论量子力学”。那是我第一次有意识地接触理论物理学。我一头扎进了 Morse 和 Feshbach 的书里,大约两个月后,就深入其中。等我看完书的时候
KB:当你说“我不是天生的机械工程师,而是一个理论物理学家”时,你是说你早年就知道自己想成为一名科学家吗?
BSR 博士:从某种意义上说,是的,尽管科学家这个词并没有特别引起我的注意。在印度,当人们谈论科学家时,他们更多指的是技术、发明或创新。他们有发明家爱迪生的想法,代表科学家的形象。我对此没有异议,只是我认为它扭曲了科学家一词的含义。科学家是一个寻求未知的人,他更喜欢发现而不是发明。嗯,我对发现更感兴趣,尽管我确实参与了许多小玩意和小发明的动手修补,大多数孩子都喜欢。但我更感兴趣的是对现象背后的哲学探索,并没有然后意识到成为一名科学家可能会导致这一点。但是,是的,即使那样,
KB:在你的工程项目中,你真正进入了理论物理。了解更多关于这一点真的很有趣,并保持网站的主题“数学现实”,您可以谈论您对理论物理学中数学美的追求。
BSR 博士:我认为数学之美对我来说是很自然的,因为我进入理论物理的方式非常规和新颖。通常,人们会从经典力学、经典电动力学、量子力学以及数学方法开始。相反,我是从广义相对论开始的!
KB:广义相对论?你怎么能做到这一点?没有你提到的分支的背景,特别是广义相对论是理论物理学中比较困难的分支之一,在博士水平之前是无法访问的。
BSR 博士:我同意,这是非常不寻常的,就我而言,这是无知战胜知识的力量之一。以我目前对认知神经科学和积极心理学的理解,我会说这是我没有像大多数学生那样接受“习得性无助”的一个例子。我的意思是,我没有被“教导”到像广义相对论这样的领域是不可能的,所以我继续去做了。怎么做并不重要,因为一旦你有了足够强的“为什么”,潜意识就会弄清楚怎么做。但我认为我偏离了我们的主题。
让我回到数学现实。所以,从广义相对论开始,我很自然地被它深刻的数学之美所震撼,霍金和以色列在他们担任编辑的书中如此精美地捕捉到了什么,“广义相对论,爱因斯坦百年调查,”
“没有人能不激动地回忆起他第一次遇到这个空间弯曲、时间为第四维的卡罗尔世界,诚实的目击者在关于发生在何时何地发生的事情的最基本问题上存在分歧。”
我第一次接触到“张量”这个词,是在杰里米·伯恩斯坦 (Jeremy Bernstein) 的著作《爱因斯坦》(Einstein) 中,我在第7次阅读后来,在我进入工程学之前的五个月期间,我阅读了 Minrosky 等人写的绝对精彩的书“空间、时间、引力”,这是 Mir 出版社的一本书。那本书真的让我一瞥,让我大开眼界,不仅是张量,还有 Elie Cartan 的外微积分、黎曼几何、芬斯勒空间、Weyl 的规范不变几何、Kaluza-Klein 理论等等。但这是在半技术层面。我很快就掌握了朗道和利夫希茨的理论物理学课程,第一卷和第二卷,分别是“力学”和“经典场论”,这是我认真学习广义相对论的开始。我接着读了彼得·伯格曼 (Peter Bergmann) 的旧书《相对论》,然后是 C 莫勒 (C Moller) 的另一本旧书《广义相对论》(General Relativity。
大约在这个时候,事情发生得相当快,而且长话短说,我开始不时会见印度班加罗尔印度科学研究所理论研究中心的 J Pasupathy 教授。他给了我史蒂文温伯格的书,“广义相对论”,我在一个月内掌握了它,然后转向霍金和埃利斯的迷人美丽的书“时空的大尺度结构”,当然还有米斯纳、索恩、惠勒的“引力。” 那是我的不归路。我永远,永远无法过平凡的生活。它把我提升到我无法想象的高度。在读那本书的几周和几个月里,我沉浸在狂喜中。它引导我从 J Kelly 的著作“General Topology”、Hocking 和 Young、“Topology”、Sigurdur Helgason、
在所有这些中,我最美妙的经历是掌握 Elie Cartan 的微分形式微积分并计算出爱因斯坦场方程的 Schwarzschild 和 Kerr 解、最大对称空间、彭罗斯 2-旋量形式主义和引力场分类, Twistor 上同调等。从某种意义上说,Elie Cartan 的作品最能唤起我的数学之美。没有什么能比得上这一点,即使在今天,我仍致力于通过多辛几何的框架来追求 Elie Cartan 工作的更深层次的影响,尤其是来自 G Sardanashvily 及其合作者 Jerrold E Marsden、Mark Gotay(GIMMSY 文章)和当然,罗伯特赫尔曼关于嘉当工作的精彩书籍。
KB:那确实是您进入理论物理学的全面视角。我自己已经掌握了 Elie Cartan 的方法,并且不得不同意你所说的。在我自己的工作中,我将辛几何应用于量子力学,确实,数学之美真的很惊人。
BSR 博士:除了对 Elie Cartan 方法的追求之外,我很快遇到了 Gauge 理论......而且......我的呼吸几乎无法说出这个......这是我一生中最迷人、最神奇的经历......意识到 Gauge 理论背后的结构和纤维束是一样的。我只能通过在他的 Endymion 中引用济慈来描述这一点,
“幸福在哪里?在那个召唤我们准备好与神圣相交的思想,与本质的团契;直到我们发光,完全炼金术,没有空间。”
我在经历这些认识和理解的过程中失去了日日夜夜的感觉。我研究理论物理的时间太长了,以至于我经常连续两天醒来,第二天才睡觉,错过了工程学院的课程。我会在梦中醒来,并迅速将我以隐喻形式收到的见解转写成文字。我无法再认同几年前的自己。我是一个转变的人,这个探索完全俘获了我,我真的很幸运,因为没有更好的词,我被赐予了这条通往理论物理学的道路。因此,对我而言,理论物理学是灵魂最深处的召唤,是英雄的旅程,是前往应许之地的冒险。雪莉的阿拉斯托或孤独的灵魂,
“以庄严的眼光和明亮的银色梦想,他的童年是被养育的。每一个景象还有来自广阔大地和周围空气的声音,将最精妙的冲动发送到他的心中。神圣哲学的源泉没有逃离他渴望的嘴唇,以及所有伟大的,或美好,或可爱,这神圣的过去无论是真实的还是寓言的奉献,他都觉得并且知道。”
KB:就像你说的那样,我感受到了精神的激荡。是的,确实如此,随着人们越来越深入理论物理学的核心,就不可能回到平凡的生活,我想这就是你说这是英雄之旅的原因。因为,正如我记得约瑟夫坎贝尔的书,“千面英雄”,英雄离开了平凡的世界,踏上了他的旅程。当他继续前进时,他犹豫不决,很多时候,感觉就像要放弃。并且介入了一个阶段,之后他知道在完成英雄的旅程之前回到普通世界是不可能的。
BSR博士:是的,你说的很准确。在我身上,从平凡的世界进入理论物理学的世界,也伴随着一种我最能称之为朴素、纯洁的感觉,好像我所有的身体、情感、精神和精神能量都被专注于追求并提供必要的火箭推进力,以摆脱普通世界的吸引力。
对我来说,理论物理学象征着进入纯粹思想和精神领域的神秘旅程,我日夜感受到我内心的深刻蜕变。数学之美很快融入了真理,然后完美无暇的宁静感降临在我身上,使我对自然法则的探索变得完全内在。所有这些感受开始带来太多无法表达、深不可测的洞见。这就是为什么,我仍然有 笔记本和床单,里面装满了我的作品和文件,无论是完成的还是未完成的,我选择让它们堆叠起来待命。您将在网站上看到的“数学现实”部分来自这些见解。
KB:我认为,如果您能用自己的话概括出著名的 CFRCE 理论与数学范式,它会澄清很多,它是您在工程时期的愿景的产物。
BSR 博士:当然,为此我必须谈谈初学者的大脑。初学者的大脑具有无限的学习可能性,因为它具有自然需要有价值挑战的潜在技能。缺乏这种挑战,初学者就会幻灭,精神能量就会分散在徒劳的努力中。因此,提供一个路线图来适应 BDNF 的巨大发射是必不可少的。
作为一个年轻的初学者,在我自己在理论物理学方面的努力的鼎盛时期,我自己面临着为自己提供一个我可以倾注全部精力的挑战的必要性。由于我无法从枯萎的文献或研究人员社区中找到任何指导,因此我尝试了几种对我也很有吸引力的方法。有一段时间,我什至完全转向纯数学,认为它最好提供我正在寻找的资源,以便认真研究理论物理。经过三四年的纯数学学习,我开始同意爱因斯坦在自传笔记中所写的内容,
“我看到数学被分成了许多专业,每个专业都可以轻松吸收我们短暂的生命。结果,我看到自己处于布里丹的屁股的位置,无法决定任何一捆干草。”
因此,虽然没有失望,但对纯数学的幻想破灭了,我回到了理论物理。但我对数学的沉浸并不是徒劳的。因为,当我回到物理学时,我发现出现了一个全新的视角。突然间,理论物理学似乎贯穿了几条线索,所有线索都从变分法开始。我希望制定一个统一的计划,为我的研究提供组织原则。当我开始画草图时,这幅画在我脑海的画布上形成,并形成了一个完整的路线图。当我把它写在纸上时,我是如此着迷,以至于我几个星期都睡不好,食欲不振。在我的工程学院的课堂上,我在发呆中走来走去,
接下来的几个月里,我在印度科学研究所的图书馆和其校园内的 TIFR 中心度过,整理原始书籍和参考资料,并从物理报告、Rivista del Nuovo Cimento、Reviews of Modern Physics、 Journal of Mathematical Physics,以及其他几本期刊,暑期学校的论文集和会议等。接下来,列出这些还不够,我需要掌握它们以免干扰我的学习。在接下来的几个月里,我设法掌握了所有这些和那些没有的,我通过直接写信给数学家和物理学家来获得它们。
我收到的最令人难忘的文章之一是来自巴黎的 Marcel Berger,“ 20 世纪下半叶的黎曼几何”。在收集所有这些之后,而不是在我收集它们的同时,我开始了我的宏伟愿景,即以统一的方式掌握理论物理和数学物理的所有基本分支,绘制出主题的各种相互关联、相互依赖和逻辑独立性。我对这些来源的研究越多,我的笔记就越长。我的工程研究逐渐减少,我开始逃学。
这种模式一直延续到我进入印度天体物理研究所,虽然我的正式论文是在古典广义相对论和黑洞中,但我继续致力于我对圈量子引力的愿景。我很快就看到其他学生开始注意到我参与的奇怪事情,为了防止被打扰,我迅速切换到夜间模式。我在学院出现的时间越来越晚,直到有一天我到达学院时,其他人要离开了。我会去图书馆整夜坐在我的徒步旅行背包里的那堆书和文件里。
这段时间,我的路线图对我来说也变得非常清晰和具体。这是我们在 CFRCE 中使用的更新版本。
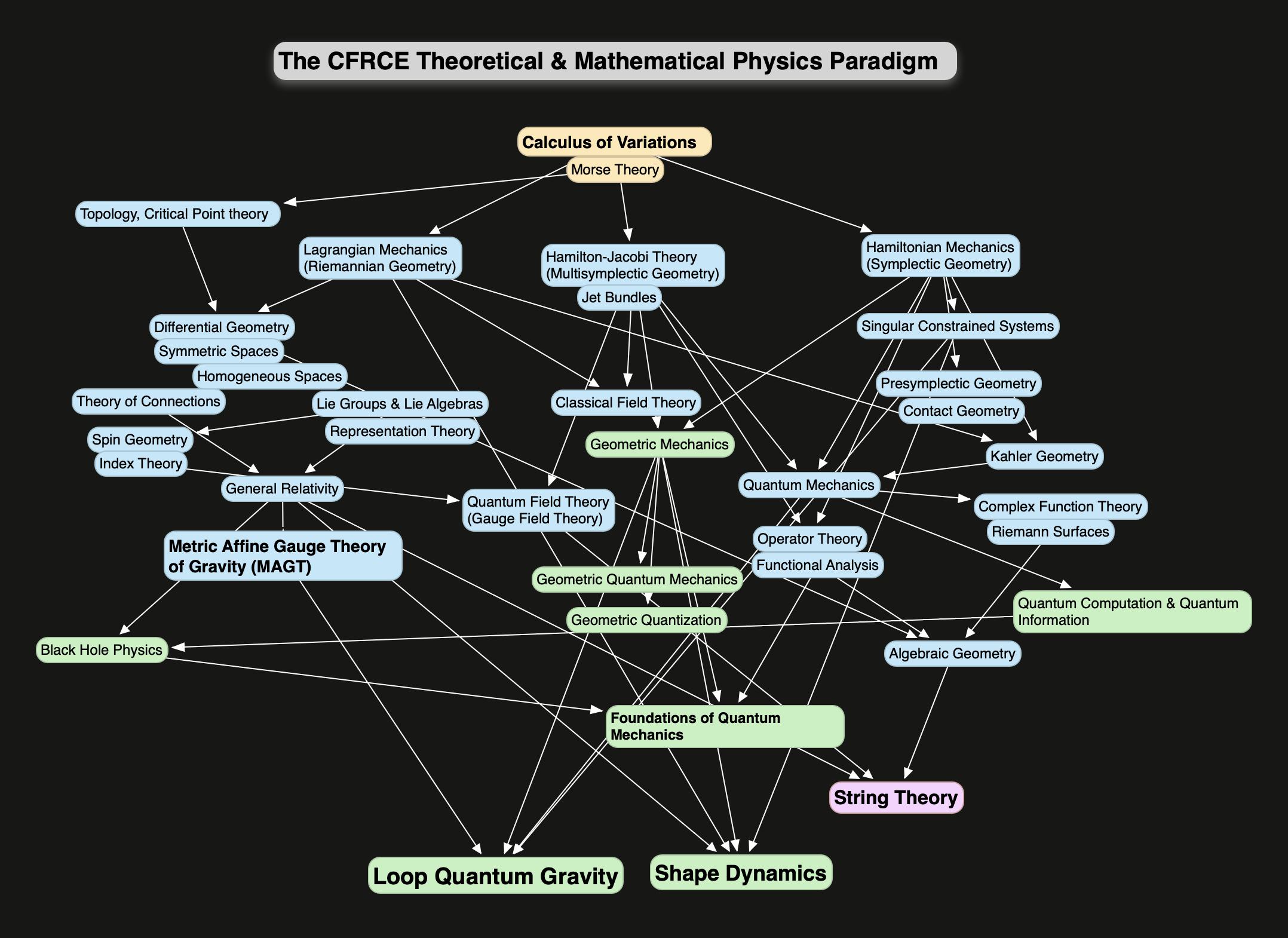
KB:你选择了某些关键主题来描绘绿色背景的方框?
BSR 博士:是的,简而言之,就是我所说的 Klein-Cartan 范式、圈量子引力、形??状动力学、几何力学、几何量子力学、几何量化、黑洞物理学和量子力学基础。我本可以添加约束量化、多辛几何、Hamilton-Jacobi 理论的几何方法、克利福德微积分、自旋几何和指数理论。但也许在我们第一次开始这件事之后。
KB:从这个网站的主题的角度给出第一个主题的想法怎么样?
BSR 博士:当然,让我们来看第一个,“Klein-Cartan 范式”。我的意思是,这是 Felix Klein 的 Erlangen 程序的现代版本,结合了 Elie Cartan 对几何学的深刻概括。在阅读了 Robert Hermann 关于变分、微分几何、Cartan-Ehresmann 联系、李理论和系统的精美著作后,我一直在朝着这个方向前进。但是,只有在我阅读了 Sharpe 的精美著作《微分几何,嘉当对克莱因 Erlangan 程序的概括》时,我才创造了 Klein-Cartan 范式这个术语。我打算采用 Klein 和 Cartan 的方法来概括理论物理学中使用的几何结构,尤其是哈密顿系统、动量图以及后来的多动量图。我还想将 de Donder 的形式主义带入其中。其实有,Neemann、Hehl、McCrea 等人在这方面的出色工作,“公制仿射引力规理论”。H Kastrup 还有另一篇深度文章,“物理学中拉格朗日动力系统的典型拉格朗日理论”。还有一些其他的文章也沿着这些方向。我想将它们结合起来制定 Klein-Cartan 范式。在我的笔记中,我概述了人们可以采取的方法,从轮换组开始,研究组扩展和上同调,概括它们,然后研究组收缩以验证离开的结果。Azcarraga 和 Izquierdo 写了一本很棒的书,“李群、李代数、上同调和物理学中的一些应用”,它为群理论构造提供了很多动力。“重力的公制仿射规范理论。” H Kastrup 还有另一篇深度文章,“物理学中拉格朗日动力系统的典型拉格朗日理论”。还有一些其他的文章也沿着这些方向。我想将它们结合起来制定 Klein-Cartan 范式。在我的笔记中,我概述了人们可以采取的方法,从轮换组开始,研究组扩展和上同调,概括它们,然后研究组收缩以验证离开的结果。Azcarraga 和 Izquierdo 写了一本很棒的书,“李群、李代数、上同调和物理学中的一些应用”,它为群理论构造提供了很多动力。“重力的公制仿射规范理论。” H Kastrup 还有另一篇深度文章,“物理学中拉格朗日动力系统的典型拉格朗日理论”。还有一些其他的文章也沿着这些方向。我想将它们结合起来制定 Klein-Cartan 范式。在我的笔记中,我概述了人们可以采取的方法,从轮换组开始,研究组扩展和上同调,概括它们,然后研究组收缩以验证离开的结果。Azcarraga 和 Izquierdo 写了一本很棒的书,“李群、李代数、上同调和物理学中的一些应用”,它为群理论构造提供了很多动力。“物理学中拉格朗日动力系统的典型拉格朗日理论。” 还有一些其他的文章也沿着这些方向。我想将它们结合起来制定 Klein-Cartan 范式。在我的笔记中,我概述了人们可以采取的方法,从轮换组开始,研究组扩展和上同调,概括它们,然后研究组收缩以验证离开的结果。Azcarraga 和 Izquierdo 写了一本很棒的书,“李群、李代数、上同调和物理学中的一些应用”,它为群理论构造提供了很多动力。“物理学中拉格朗日动力系统的典型拉格朗日理论。” 还有一些其他的文章也沿着这些方向。我想将它们结合起来制定 Klein-Cartan 范式。在我的笔记中,我概述了人们可以采取的方法,从轮换组开始,研究组扩展和上同调,概括它们,然后研究组收缩以验证离开的结果。Azcarraga 和 Izquierdo 写了一本很棒的书,“李群、李代数、上同调和物理学中的一些应用”,它为群理论构造提供了很多动力。我已经概述了可以采取的方法,从轮换组开始,研究组扩展和上同调,概括它们,然后研究组收缩以验证离开的结果。Azcarraga 和 Izquierdo 写了一本很棒的书,“李群、李代数、上同调和物理学中的一些应用”,它为群理论构造提供了很多动力。我已经概述了可以采取的方法,从轮换组开始,研究组扩展和上同调,概括它们,然后研究组收缩以验证离开的结果。Azcarraga 和 Izquierdo 写了一本很棒的书,“李群、李代数、上同调和物理学中的一些应用”,它为群理论构造提供了很多动力。
KB:太好了,这是一个非常好的主意。您已经简洁地说明了“数学现实”的目的。因此,我们现在可以将热心的读者推荐给该网站,以了解理论物理的真、美、宁静和洞察力!无论如何,我们计划本着“实时评论”的精神不断更新该网站。
BSR 博士:是的,就是这样。正如您所建议的,我们会根据我们想要分享的新见解和观点不断更新它。
KB:还有相关的博客,您将在其中更定期地发布您的见解和观点。
BSR 博士:我想这样做。




