-*-紫色王家思絮絮-*-
我思无邪、我行无悔
正文
先说明一下,这里的圆锥曲线,也称为二次曲线,就是大家所熟知的椭圆、抛物线以及双曲线的统称,这是中学数学中的平面解析几何的主要内容,相信大家都还记 得。历史上第一位对圆锥曲线作出系统研究的是古希腊大拿阿波罗尼斯,他老人家将圆锥曲线的主要性质几乎一网打尽,直到一千多年后笛卡儿创立了解析几何才有 了质的改变。温习一下,我们有:
椭圆 (&圆 as a special case):x^2/a^2 + y^2/b^2 = 1;
双曲线:x^2/a^2 - y^2/b^2 = 1;
抛物线:y^2 = 2ax
这些 (由定义导出的) 公式,相信大家都记得,即使是成色十足的文科大拿也应该记得。另外再说明一下,为了后文表述的简洁,我们假设空间是一维的,以 x 标记;时间自然是一维的 (当然如果是 2 维或者以上,那现在大约只有供大家在哲学上胡掰的意义),以 t 标记。光速不变是指狭义相对论意义下的真空中惯性参照系中的光速不变;或者从广义相对论的角度来说,是指某个“点”附近的平直空间满足络伦兹变换 (理解这点可能稍微困难一点,但是却是至关重要的,建议蒙古物理学家们仔细体会)。
好了,有了这些铺垫,俺们从初等几何的观点出发,来考察“光速不变”以及相关话题 (例如因果律) 的几何意义。尽管咱们只涉及初等几何,但会涉及到非欧几何,所以对许多蒙古数学家和蒙古物理学家而言,某些表述可能会有点陌生。涉及非欧几何的部分,俺想 了想,将在下集里集中表述。
在闲侃 (1) 中咱们说过,在看起来非常合理的假设下,从变换群的观点出发,可以推理出咱们这个物理世界的运动速度必须对应以下三种情形之一:
a) 速度可以是任意值;特别,速度的最大值是无穷大;
b) 速度存在个上限值;
c) 速度存在个下限值。
不同的情形对应着不同的时空;从几何观点看,也对应着不同的几何。对最简单的 a) 而言,大家知道,相应的时空变换是迦利略变换,对应着牛顿经典力学,在不同的参照系中,t1 = t2,完全和空间无关,时间是绝对的;若不考虑时间部分,其对应的几何就是大家最熟悉的欧几里得几何;但若考虑两维时空 (as a whole,记住这里咱们约定了,为了表述简单,只考虑一维空间),迦利略变换对应的几何不是欧几里得几何,而是一种比欧几里得几何更简单的几何:迦利略 几何。迦利略几何之所以比欧几里得几何更简单,是因为前者涉及到角度的转动时,其对应的转动几何量是能直接线性相加减的,而欧几里得几何则和三角函数有 关,例如在欧几里得几何中,我们有关于三角形的正弦定理:a/sinA = b/sinB =c/sinC,而在迦利略几何中其对应的正弦定理就退化成 trivial 的形式:a/A=b/B=c/C。
我们重点介绍 b),对应于咱们的物理世界,以及 c),对应于某种假想的、不存在的物理世界。这里俺之所以也讨论 c),是因为:
1) 好奇 (俺自己用初等数学推导了一下相应的变换,俺好奇它到底对应着什么);
2) 和 a)、b) 类比,从非欧几何的角度,能系统地阐述 a)、b)、c);
3) 广义相对论框架下可能潜在的物理意义。这点往往会被人忽视,但如本文开头所说的,络伦兹变换 (考虑动力学内容,就是狭义相对论) 本质上是广义相对论几何表述下的一个 component,亦即局域平直空间所遵循的坐标变换。既然狭义相对论只是广义相对论局域上所要求的,这就使得在大范围考虑物理 (当然,这主要是宇宙学方面的内容了) 时,就至少在理论上存在 A 处和 B 处的几何空间/局域坐标变换不同的可能 (当然,迦利略变换也是 choice 之一)。当然,这个考虑看起来有点匪夷所思 (主要是其物理意义看起来很牵强附会)。
b) 对应大家熟悉的络伦兹变换 (rescale 使得最大速度 -- 光速 = 1):
t1 = a*( t - v*x)
x1 = a*(-v*t + x)
这里 a = 1/sqrt(1-v^2),就是所谓的洛伦兹因子。因为 v < 1,所以 a > 1,无须赘述。
现在我们开始看因果律。哲学上的因果律自然是众说纷纭,例如大哲学家、数理逻辑学家罗素 (就是以哲学散文获得诺贝尔文学奖的那位) 就这样描述:“因果律是一个普遍原理,在已知关于某些时空领域的充分数据的条件下,凭借这个原理我们可以推论出关于某些其它时空领域的若干情况”,但是在 物理上,因果律特别是经典的因果律,有一个严谨的表述,那就是,如果两个事件有“因果关系”,“因事件”发生在前,“果事件”发生在后,假设“因果”时间 上相差 10 秒,那么在另一参照系 (这里指惯性参照系) 中的观测者来看,尽管“因果”时间上相差可以不是 10 秒,但是因果的先后秩序是不变的,绝对不会出现“果事件”在前发生的情况。也就是说,“因果律”的数学符号 (正数、负数或者 0) 是个不变量。
显然,因果律在哲学上、物理上都是重大的话题。例如假设我看到的是北韩先向南韩发射一枚导 弹,然后看到导弹在首尔爆炸,而你看到的却是导弹先在首尔爆炸,然后才看到北韩先南韩发射那枚导弹,那会如何?历史上,尽管因果律显然是最重要的话题之 一,但是物理学却几乎没有相应的理论专门讨论因果律,就算是现在“公理化物理”大行其道的今天,也几乎没有什么理论将它作为前提条件提出来。当然,我想这 其中最大的理由就是,在经典物理里,因果律从来就不是问题 (因为绝对时间的存在);在狭义相对论里,它也不是问题,至少在咱们这个物理世界,它也不是问题 (等下我们看看这句话到底是什么意思)。在物理学上,经典的因果律主要在以下两种情形出问题:
1) 广义相对论;
2) 量子力学。
噢~~喔......,大家看到麻烦了么?尽管因果律主要只在两种情形下出问题,但是出问 题的广义相对论和量子力学偏偏是现代物理最重要的理论。不过,好在现代物理学的另一根基,狭义相对论,还能严格遵守因果律;而广义相对论对因果律的违背, 本质上是因为几何描述是非平直空间的结果,理论上它是可以计算、追踪的,所以至少在本源上,这不是多大的问题,但是在量子力学中,这种对经典因果律的违背 却是本质的,不可解的 (例如著名的薛定愕猫)。历史上,这是以爱因斯坦和波尔之间的世纪论战所争论的主要话题之一。追求唯美的爱因斯坦不能忍受经典的因果律在物理学中得以破 坏。
从上面给出的络伦兹变换公式可以简单地证明:
t1^2 - x1^2 = t^2 - x^2 = B
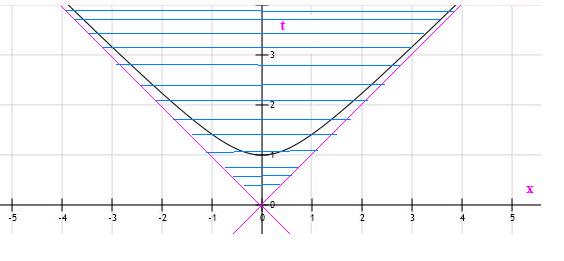
也就是说,在不同的惯性参照系下,t^2 - x^2 是个不变量 B (注意我们已经将光速 c 定义为 1)。t^2 - x^2 = B = const 是啥?双曲线,对不对?因为我们已经假设了 c 是所有物体运动速度的上限,所以对有物理意义的事件而言,它只可能存在于 |t| >= |x| 的区域,也就是下图中画阴影部分的那个三角形区域 (当然,若考虑三维空间,这个三角形区域将会是个圆锥),而红线则是双曲线 t^2 - x^2 = B > 0 的渐进线,很明显,其斜率 = 1 就是光速。而空白区域 (非阴影部分,当然这里我们限于 t >= 0) 则是没有物理意义的区域。数学上可以简单地证明,对阴影部分的任何事件而言,经典的因果律是严格得以遵守的,而这正是爱因斯坦质疑哥本哈根学派的主要理由 之一。
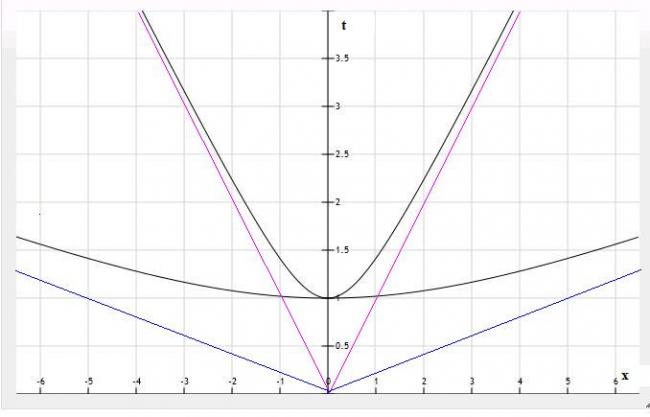
如果光速增加 5 倍呢?如果光速增加 5 倍,在同一 scale 下,那么有物理意义的区域就是斜率 = 1/5 或者 -1/5 两条直线 (图中的蓝色直线) 之上的区域,很明显这比红色区域要大。如果光速无限地增加到无穷大,那么 b) 就退化到情形 a),络仑兹变换就退化到加利略变换,所有的区域都是有物理意义的,因果律都得以遵守 ---- 这也是历史上因果律不那么重要、没有很早就摆到台面的原因(之一):因为它根本不是问题。
那么 Case c) 对应啥?这和咱们的物理世界不符合 (因为它要求在任何惯性参照系下,物体的运动速度都会大于或者等于某个定值),但是它的数学描述却是应该有的。俺没有找到相关的描述,但是好在从 c) 出发,推导出相应的变换公式不难,俺就边码字边推导,结果如下 (无伤大雅地,咱们这里也称之为“络仑兹变换”):
t1 = b * ( t + v*x)
x1 = b * (-v*t + x)
b = 1/sqrt (1+v^2),这里 v 是速度,最小速度 d 已经设为 1,自然根据假定,v >= d = 1,所以“络仑兹因子” b <= sqrt(2)/2。
很容易证明,在上述“络仑兹变换”下,二维时空的平方和
t^2 + x^2 = B = const
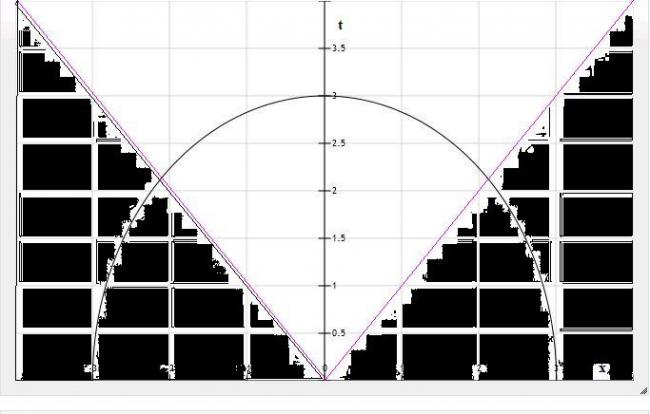
是个不变量。对有物理意义的事件而言,它只可能存在于 |t| <= |x| 的区域,也就是下图中画阴影部分的那两个三角形区域 (若考虑三维空间,这两个三角形区域,会是一个圆柱挖去一个圆锥),而红线斜率 = 1 (or -1) 就是最小速度。而空白区域 (非阴影部分,当然这里我们限于 t >= 0) 则是没有物理意义的区域。数学上可以类似地证明,对阴影部分的任何事件而言,经典的因果律也是严格得以遵守的。
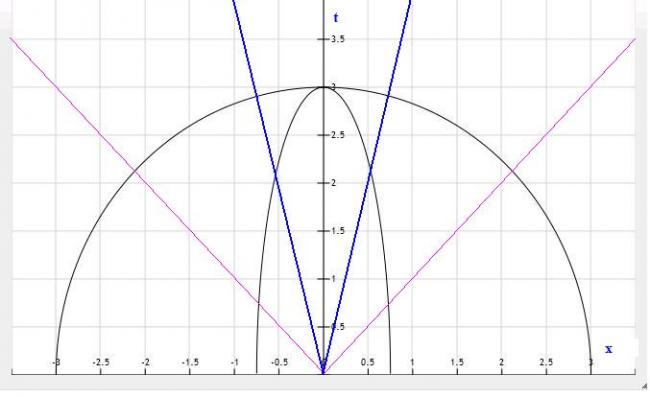
如果最小速度减少 4 倍呢?如果最小速度减少 4 倍,在同一 scale 下,那么有物理意义的区域就是斜率 = 4 或者 -4 两条直线 (图中的蓝色直线) 之下的区域,很明显这比红色区域要大。如果最小速度减少到 0,那么 c) 就退化到情形 a),“络仑兹变换”就退化到加利略变换,所有的区域都是有物理意义的,因果律都得以遵守。
接下来我们来看三种时空变换下对应的几何是什么。咱们的结论是:
a) 对应于加利略几何 (比欧几里得几何更简单的几何,属于非欧几何的一种);
b) 对应于闵可夫斯基几何 (自然也属于非欧几何的一种);
c) 对应于通常的欧几里得几何。
具体如何,且听下回分解。今天俺累死了。 - See more at: http://blog.creaders.net/jingjibird628/user_blog_diary.php?did=153455#sthash.GePiayIU.dpuf
椭圆 (&圆 as a special case):x^2/a^2 + y^2/b^2 = 1;
双曲线:x^2/a^2 - y^2/b^2 = 1;
抛物线:y^2 = 2ax
这些 (由定义导出的) 公式,相信大家都记得,即使是成色十足的文科大拿也应该记得。另外再说明一下,为了后文表述的简洁,我们假设空间是一维的,以 x 标记;时间自然是一维的 (当然如果是 2 维或者以上,那现在大约只有供大家在哲学上胡掰的意义),以 t 标记。光速不变是指狭义相对论意义下的真空中惯性参照系中的光速不变;或者从广义相对论的角度来说,是指某个“点”附近的平直空间满足络伦兹变换 (理解这点可能稍微困难一点,但是却是至关重要的,建议蒙古物理学家们仔细体会)。
好了,有了这些铺垫,俺们从初等几何的观点出发,来考察“光速不变”以及相关话题 (例如因果律) 的几何意义。尽管咱们只涉及初等几何,但会涉及到非欧几何,所以对许多蒙古数学家和蒙古物理学家而言,某些表述可能会有点陌生。涉及非欧几何的部分,俺想 了想,将在下集里集中表述。
在闲侃 (1) 中咱们说过,在看起来非常合理的假设下,从变换群的观点出发,可以推理出咱们这个物理世界的运动速度必须对应以下三种情形之一:
a) 速度可以是任意值;特别,速度的最大值是无穷大;
b) 速度存在个上限值;
c) 速度存在个下限值。
不同的情形对应着不同的时空;从几何观点看,也对应着不同的几何。对最简单的 a) 而言,大家知道,相应的时空变换是迦利略变换,对应着牛顿经典力学,在不同的参照系中,t1 = t2,完全和空间无关,时间是绝对的;若不考虑时间部分,其对应的几何就是大家最熟悉的欧几里得几何;但若考虑两维时空 (as a whole,记住这里咱们约定了,为了表述简单,只考虑一维空间),迦利略变换对应的几何不是欧几里得几何,而是一种比欧几里得几何更简单的几何:迦利略 几何。迦利略几何之所以比欧几里得几何更简单,是因为前者涉及到角度的转动时,其对应的转动几何量是能直接线性相加减的,而欧几里得几何则和三角函数有 关,例如在欧几里得几何中,我们有关于三角形的正弦定理:a/sinA = b/sinB =c/sinC,而在迦利略几何中其对应的正弦定理就退化成 trivial 的形式:a/A=b/B=c/C。
我们重点介绍 b),对应于咱们的物理世界,以及 c),对应于某种假想的、不存在的物理世界。这里俺之所以也讨论 c),是因为:
1) 好奇 (俺自己用初等数学推导了一下相应的变换,俺好奇它到底对应着什么);
2) 和 a)、b) 类比,从非欧几何的角度,能系统地阐述 a)、b)、c);
3) 广义相对论框架下可能潜在的物理意义。这点往往会被人忽视,但如本文开头所说的,络伦兹变换 (考虑动力学内容,就是狭义相对论) 本质上是广义相对论几何表述下的一个 component,亦即局域平直空间所遵循的坐标变换。既然狭义相对论只是广义相对论局域上所要求的,这就使得在大范围考虑物理 (当然,这主要是宇宙学方面的内容了) 时,就至少在理论上存在 A 处和 B 处的几何空间/局域坐标变换不同的可能 (当然,迦利略变换也是 choice 之一)。当然,这个考虑看起来有点匪夷所思 (主要是其物理意义看起来很牵强附会)。
b) 对应大家熟悉的络伦兹变换 (rescale 使得最大速度 -- 光速 = 1):
t1 = a*( t - v*x)
x1 = a*(-v*t + x)
这里 a = 1/sqrt(1-v^2),就是所谓的洛伦兹因子。因为 v < 1,所以 a > 1,无须赘述。
现在我们开始看因果律。哲学上的因果律自然是众说纷纭,例如大哲学家、数理逻辑学家罗素 (就是以哲学散文获得诺贝尔文学奖的那位) 就这样描述:“因果律是一个普遍原理,在已知关于某些时空领域的充分数据的条件下,凭借这个原理我们可以推论出关于某些其它时空领域的若干情况”,但是在 物理上,因果律特别是经典的因果律,有一个严谨的表述,那就是,如果两个事件有“因果关系”,“因事件”发生在前,“果事件”发生在后,假设“因果”时间 上相差 10 秒,那么在另一参照系 (这里指惯性参照系) 中的观测者来看,尽管“因果”时间上相差可以不是 10 秒,但是因果的先后秩序是不变的,绝对不会出现“果事件”在前发生的情况。也就是说,“因果律”的数学符号 (正数、负数或者 0) 是个不变量。
显然,因果律在哲学上、物理上都是重大的话题。例如假设我看到的是北韩先向南韩发射一枚导 弹,然后看到导弹在首尔爆炸,而你看到的却是导弹先在首尔爆炸,然后才看到北韩先南韩发射那枚导弹,那会如何?历史上,尽管因果律显然是最重要的话题之 一,但是物理学却几乎没有相应的理论专门讨论因果律,就算是现在“公理化物理”大行其道的今天,也几乎没有什么理论将它作为前提条件提出来。当然,我想这 其中最大的理由就是,在经典物理里,因果律从来就不是问题 (因为绝对时间的存在);在狭义相对论里,它也不是问题,至少在咱们这个物理世界,它也不是问题 (等下我们看看这句话到底是什么意思)。在物理学上,经典的因果律主要在以下两种情形出问题:
1) 广义相对论;
2) 量子力学。
噢~~喔......,大家看到麻烦了么?尽管因果律主要只在两种情形下出问题,但是出问 题的广义相对论和量子力学偏偏是现代物理最重要的理论。不过,好在现代物理学的另一根基,狭义相对论,还能严格遵守因果律;而广义相对论对因果律的违背, 本质上是因为几何描述是非平直空间的结果,理论上它是可以计算、追踪的,所以至少在本源上,这不是多大的问题,但是在量子力学中,这种对经典因果律的违背 却是本质的,不可解的 (例如著名的薛定愕猫)。历史上,这是以爱因斯坦和波尔之间的世纪论战所争论的主要话题之一。追求唯美的爱因斯坦不能忍受经典的因果律在物理学中得以破 坏。
从上面给出的络伦兹变换公式可以简单地证明:
t1^2 - x1^2 = t^2 - x^2 = B
也就是说,在不同的惯性参照系下,t^2 - x^2 是个不变量 B (注意我们已经将光速 c 定义为 1)。t^2 - x^2 = B = const 是啥?双曲线,对不对?因为我们已经假设了 c 是所有物体运动速度的上限,所以对有物理意义的事件而言,它只可能存在于 |t| >= |x| 的区域,也就是下图中画阴影部分的那个三角形区域 (当然,若考虑三维空间,这个三角形区域将会是个圆锥),而红线则是双曲线 t^2 - x^2 = B > 0 的渐进线,很明显,其斜率 = 1 就是光速。而空白区域 (非阴影部分,当然这里我们限于 t >= 0) 则是没有物理意义的区域。数学上可以简单地证明,对阴影部分的任何事件而言,经典的因果律是严格得以遵守的,而这正是爱因斯坦质疑哥本哈根学派的主要理由 之一。

如果光速增加 5 倍呢?如果光速增加 5 倍,在同一 scale 下,那么有物理意义的区域就是斜率 = 1/5 或者 -1/5 两条直线 (图中的蓝色直线) 之上的区域,很明显这比红色区域要大。如果光速无限地增加到无穷大,那么 b) 就退化到情形 a),络仑兹变换就退化到加利略变换,所有的区域都是有物理意义的,因果律都得以遵守 ---- 这也是历史上因果律不那么重要、没有很早就摆到台面的原因(之一):因为它根本不是问题。

那么 Case c) 对应啥?这和咱们的物理世界不符合 (因为它要求在任何惯性参照系下,物体的运动速度都会大于或者等于某个定值),但是它的数学描述却是应该有的。俺没有找到相关的描述,但是好在从 c) 出发,推导出相应的变换公式不难,俺就边码字边推导,结果如下 (无伤大雅地,咱们这里也称之为“络仑兹变换”):
t1 = b * ( t + v*x)
x1 = b * (-v*t + x)
b = 1/sqrt (1+v^2),这里 v 是速度,最小速度 d 已经设为 1,自然根据假定,v >= d = 1,所以“络仑兹因子” b <= sqrt(2)/2。
很容易证明,在上述“络仑兹变换”下,二维时空的平方和
t^2 + x^2 = B = const
是个不变量。对有物理意义的事件而言,它只可能存在于 |t| <= |x| 的区域,也就是下图中画阴影部分的那两个三角形区域 (若考虑三维空间,这两个三角形区域,会是一个圆柱挖去一个圆锥),而红线斜率 = 1 (or -1) 就是最小速度。而空白区域 (非阴影部分,当然这里我们限于 t >= 0) 则是没有物理意义的区域。数学上可以类似地证明,对阴影部分的任何事件而言,经典的因果律也是严格得以遵守的。

如果最小速度减少 4 倍呢?如果最小速度减少 4 倍,在同一 scale 下,那么有物理意义的区域就是斜率 = 4 或者 -4 两条直线 (图中的蓝色直线) 之下的区域,很明显这比红色区域要大。如果最小速度减少到 0,那么 c) 就退化到情形 a),“络仑兹变换”就退化到加利略变换,所有的区域都是有物理意义的,因果律都得以遵守。

接下来我们来看三种时空变换下对应的几何是什么。咱们的结论是:
a) 对应于加利略几何 (比欧几里得几何更简单的几何,属于非欧几何的一种);
b) 对应于闵可夫斯基几何 (自然也属于非欧几何的一种);
c) 对应于通常的欧几里得几何。
具体如何,且听下回分解。今天俺累死了。 - See more at: http://blog.creaders.net/jingjibird628/user_blog_diary.php?did=153455#sthash.GePiayIU.dpuf
评论
目前还没有任何评论
登录后才可评论.




