昨天发表了对美国实际感染人数的一个推断。主要目的是提供一个信息。我认为知情是战胜疫情与心理安稳的一个重要因素,如同知己知彼与鞋子落地一样的效应。
发表之后,有网名“刁小山”与“山水一程歌”对此有些不适,不管用意如何,我想做一正面回答,更重要的是与众多网友做一沟通和探讨。同时介绍一下有关统计与概率知识。
推断统计学(INFERENCE STATISTICS)是统计学的一个重要分支。主要目的是依据可得的数据或统计实验结果来对整体特性做出某种概率判断。类似于我们日常生活中根据某些丝蛛马迹来推断事实真相的一种思维方法。但方法是基于严格的科学推断来进行的。
推断统计学发展于二战时期。当时,盟军召集了一批优秀的概率与统计大师,根据常常是不完全或模糊的情报来推断德军的军情或用于其它军事目的。例如前几年中国有个作文考试题提到的著名统计学家WALD提出在哪里加强飞机而使其不易被击落的例子就是其中一个例子。可能另一个更加著名的例子是所谓的“德国坦克车”的问题。当时,德国坦克非常厉害,联军非常想知道德国每月能生产多少坦克车。在一个战役里,缴获了若干辆坦克车,这样就可以知道这些坦克车的生产序列号(SERIAL NUMBERS)。根据这些不完全的数据,利用概率理论,成功地估计了德国当时坦克车的月产量,和后来解密数据有很好的吻合:
月份 当时的统计推断 后来解密的数据
1940年6月 169辆/月 122辆/月
1941年6月 244辆/月 271辆/月
1942年8月 327辆/月 342辆/月
除军事方面,目前推断统计学已经用于科学研究,生产实践,与日常生活中的方方面面。比如药物的双盲实验,生产中产品的合格率与质量验收和监控,民意调查等等方面。
我所作的统计估计就是依据这样的思路所做的。我们知道美国总人口的数目,知道做了多少检测,知道其中确诊人数是多少,问题是在总人口中感染人数是多少 (注意,这不是一个简单的比例问题)。利用统计概率的思路而做出的从已知到未知的统计推断。
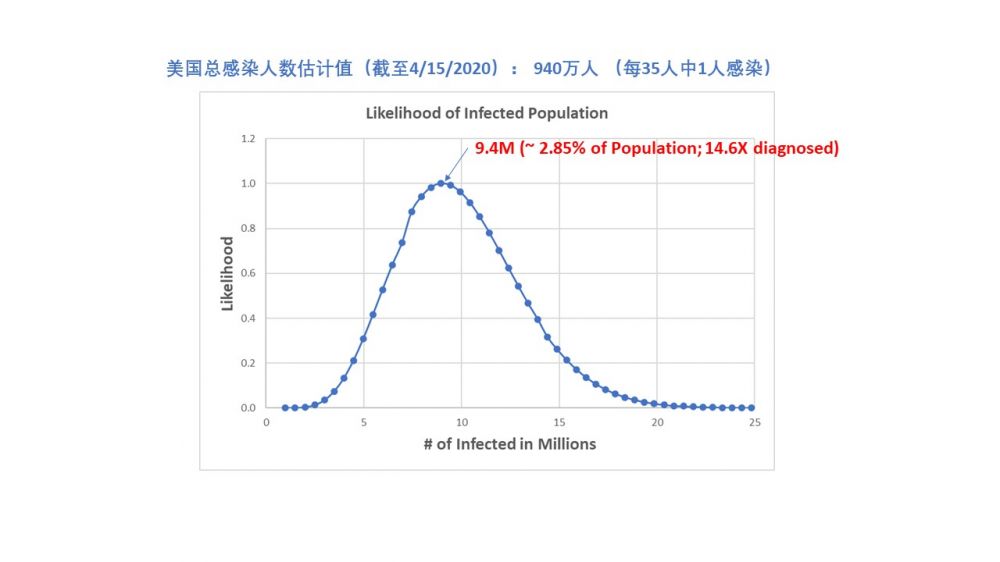
下图中是对结果的一个总结。横坐标表示的是可能的感染人数,纵坐标是每个可能感染人数的可能性。在9.4M处可能性最大。也就是说,对美国的数据来说,当感染人数是9.4M才最可能有我们看到的确诊人数。作为一个例子,而当感染人数是6M或13M时候,他们的可信性是50%。我们取最可信的9.4M作为我们最佳判断。这一结果与其它方法得出的结果和我们基于常识的直觉判断基本吻合。
很可能某些机构有些复杂的模型,有个大程序来计算。我相信简明才是事务的本原与本质。一个复杂的大MODEL,连计算的人都不知道里面运行的是什么,太复杂了,不容易抓住事物的本质。一个简明的抓住问题本质的分析,会更加可靠。